Hostname: page-component-cd9895bd7-dzt6s Total loading time: 0 Render date: 2024-12-24T12:14:50.714Z Has data issue: false hasContentIssue false
  • English
  • Français

ON A CONJECTURE OF IGUSA

Part of: Local theory Exponential sums and character sums Forms and linear algebraic groups Arithmetic problems. Diophantine geometry

Published online by Cambridge University Press:  07 February 2013

Ben Lichtin
Ben Lichtin*
Affiliation:
49 Boardman St., Rochester, NY 14607, U.S.A. (email: [email protected])
Get access

Abstract

In his Tata Lecture Notes, Igusa conjectured the validity of a strong uniformity in the decay of complete exponential sums modulo powers of a prime number and determined by a homogeneous polynomial. This was proved for non-degenerate forms by Denef–Sperber and then by Cluckers for weighted homogeneous non-degenerate forms. In a recent preprint, Wright has proved this for degenerate binary forms. We give a different proof of Wright’s result that seems to be simpler and relies upon basic estimates for exponential sums mod 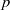$p$as well as a type of resolution of singularities with good reduction in the sense of Denef.

MSC classification

Secondary: 11L07: Estimates on exponential sums 11E95: $p$-adic theory 11E76: Forms of degree higher than two 14B05: Singularities 14G10: Zeta-functions and related questions (Birch-Swinnerton-Dyer conjecture)
Type
Research Article
Information
Mathematika , Volume 59 , Issue 2 , July 2013 , pp. 399 - 425
Copyright
Copyright © 2013 University College London 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

[1]Adolphson, A. and Sperber, S., Exponential sums and Newton polyhedra: cohomology and estimates. Ann. of Math. (2) 130 (1989), 367–406.CrossRefGoogle Scholar
[2]Cluckers, R., Igusa and Denef–Sperber conjectures on nondegenerate $p$-adic exponential sums. Duke Math. J. 141 (2008), 205–216.CrossRefGoogle Scholar
[3]Cluckers, R., Igusa’s conjecture on exponential sums modulo $p$ and $p^2$ and the motivic oscillation index. Int. Math. Res. Not. IMRN 2008 (2008), doi:10.1093/imrn/rnm118.Google Scholar
[4]Cluckers, R., Exponential sums: questions by Denef, Sperber, and Igusa. Trans. Amer. Math. Soc. 362 (2010), 3745–3756.CrossRefGoogle Scholar
[5]Cochrane, T., Bounds on complete exponential sums. In Analytic Number Theory, Vol. 1 (Progress in Mathematics 138), Birkhäuser (1996), 211–224.CrossRefGoogle Scholar
[6]Denef, J., On the degree of Igusa’s local zeta function. Amer. J. Math. 109 (1987), 991–1008.CrossRefGoogle Scholar
[7]Denef, J. and Sperber, S., Exponential sums mod $p^n$ and Newton polyhedra. Bull. Belg. Math. Soc. Simon Stevin (2001), 55–63 (suppl.).Google Scholar
[8]Heath-Brown, R. and Konyagin, S., New bounds for Gauss sums derived from $k$th powers, and for Heibronn’s exponential sum. Q. J. Math. 51 (2000), 221–235.CrossRefGoogle Scholar
[9]Igusa, J.-I., Forms of Higher Degree (Tata Institute Lectures 59), Springer (1978).Google Scholar
[10]Katz, N., Estimates for “singular” exponential sums. Int. Math. Res. Not. IMRN 16 (1999), 875–899.CrossRefGoogle Scholar
[11]Koblitz, N., $p$-adic Numbers, $p$-adic Analysis, and Zeta-Functions (Graduate Texts in Mathematics 58), Springer (1984).CrossRefGoogle Scholar
[12]Wright, J., Exponential sums and polynomial congruences in two variables: the quasi-homogeneous case. Preprint, 2012, arXiv:1202.2686.Google Scholar