Hostname: page-component-cd9895bd7-7cvxr Total loading time: 0 Render date: 2024-12-23T19:30:55.821Z Has data issue: false hasContentIssue false
  • English
  • Français

A VARIATION ON SELBERG’S APPROXIMATION PROBLEM

Part of: Linear function spaces and their duals Special classes of linear operators Harmonic analysis in one variable Spaces and algebras of analytic functions Entire and meromorphic functions, and related topics

Published online by Cambridge University Press:  14 August 2014

Michael Kelly
Michael Kelly*
Affiliation:
Department of Mathematics, University of Texas, Austin, TX 78712, U.S.A. email [email protected]
Get access

Abstract

Let 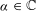${\it\alpha}\in \mathbb{C}$ in the upper half-plane and let 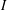$I$ be an interval. We construct an analogue of Selberg’s majorant of the characteristic function of 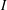$I$ that vanishes at the point ${\it\alpha}$. The construction is based on the solution to an extremal problem with positivity and interpolation constraints. Moreover, the passage from the auxiliary extremal problem to the construction of Selberg’s function with vanishing is easily adapted to provide analogous “majorants with vanishing” for any Beurling–Selberg majorant.

MSC classification

Primary: 42A05: Trigonometric polynomials, inequalities, extremal problems 42A85: Convolution, factorization 30D15: Special classes of entire functions and growth estimates 30H99: None of the above, but in this section 46E22: Hilbert spaces with reproducing kernels (=
Secondary: 47B32: Operators in reproducing-kernel Hilbert spaces (including de Branges, de Branges-Rovnyak, and other structured spaces)
Type
Research Article
Information
Mathematika , Volume 61 , Issue 1 , January 2015 , pp. 213 - 235
Copyright
Copyright © University College London 2014 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Barton, J. T., Montgomery, H. L. and Vaaler, J. D., Note on a Diophantine inequality in several variables. Proc. Amer. Math. Soc. 129(2) 2001, 337–345 (electronic).Google Scholar
Boas, R. P. Jr, Entire Functions, Academic Press (New York, 1954).Google Scholar
Bombieri, E., A note on the large sieve. Acta Arith. 18 1971, 401–404.Google Scholar
Carneiro, E. and Chandee, V., Bounding 𝜁(s) in the critical strip. J. Number Theory 131(3) 2011, 363–384.CrossRefGoogle Scholar
Carneiro, E. and Littmann, F., Bandlimited approximations to the truncated Gaussian and applications. Constr. Approx. 38(1) 2013, 19–57.Google Scholar
Carneiro, E. and Littmann, F., Entire approximations for a class of truncated and odd functions. J. Fourier Anal. Appl. 19(5) 2013, 967–996.Google Scholar
Carneiro, E., Littmann, F. and Vaaler, J. D., Gaussian subordination for the Beurling–Selberg extremal problem. Trans. Amer. Math. Soc. 365(7) 2013, 3493–3534.Google Scholar
Carneiro, E. and Vaaler, J. D., Some extremal functions in Fourier analysis. II. Trans. Amer. Math. Soc. 362(11) 2010, 5803–5843.Google Scholar
Carneiro, E. and Vaaler, J. D., Some extremal functions in Fourier analysis. III. Constr. Approx. 31(2) 2010, 259–288.Google Scholar
Chandee, V. and Soundararajan, K., Bounding |𝜁(1∕2 + i t)| on the Riemann hypothesis. Bull. Lond. Math. Soc. 43(2) 2011, 243–250.Google Scholar
de Branges, L., Hilbert Spaces of Entire Functions, Prentice-Hall (Englewood Cliffs, NJ, 1968).Google Scholar
Graham, S. W. and Vaaler, J. D., A class of extremal functions for the Fourier transform. Trans. Amer. Math. Soc. 265(1) 1981, 283–302.CrossRefGoogle Scholar
Holt, J. J. and Vaaler, J. D., The Beurling–Selberg extremal functions for a ball in Euclidean space. Duke Math. J. 83(1) 1996, 202–248.CrossRefGoogle Scholar
Hörmander, L., Distribution theory and Fourier analysis. In The Analysis of Linear Partial Differential Operators. I (Grundlehren der Mathematischen Wissenschaften [Fundamental Principles of Mathematical Sciences] 256), Springer (Berlin, 1983).Google Scholar
Lagarias, J. C., Hilbert spaces of entire functions and Dirichlet L-functions. In Frontiers in Number Theory, Physics, and Geometry. I, Springer (Berlin, 2006), 365–377.Google Scholar
Li, X.-J., On reproducing kernel Hilbert spaces of polynomials. Math. Nachr. 185 1997, 115–148.Google Scholar
Li, X.-J., A note on the weighted Hilbert’s inequality. Proc. Amer. Math. Soc. 133(4) 2005, 1165–1173 (electronic).CrossRefGoogle Scholar
Li, X.-J. and Vaaler, J. D., Some trigonometric extremal functions and the Erdős–Turán type inequalities. Indiana Univ. Math. J. 48(1) 1999, 183–236.Google Scholar
Littmann, F., Entire approximations to the truncated powers. Constr. Approx. 22(2) 2005, 273–295.Google Scholar
Littmann, F., Entire majorants via Euler–Maclaurin summation. Trans. Amer. Math. Soc. 358(7) 2006, 2821–2836 (electronic).Google Scholar
Littmann, F., One-sided approximation by entire functions. J. Approx. Theory 141(1) 2006, 1–7.Google Scholar
Littmann, F., Interpolation and approximation by entire functions. In Approximation Theory XII: San Antonio 2007 (Modern Methods in Mathematics), Nashboro Press (Brentwood, TN, 2008), 243–255.Google Scholar
Littmann, F., Zeros of Bernoulli-type functions and best approximations. J. Approx. Theory 161(1) 2009, 213–225.Google Scholar
Littmann, F., L 1-approximation to Laplace transforms of signed measures. J. Approx. Theory 163(10) 2011, 1492–1508.Google Scholar
Littmann, F., Quadrature and extremal bandlimited functions. SIAM J. Math. Anal. 45(2) 2013, 732–747.Google Scholar
Littmann, F. and Spanier, M., Extremal functions with vanishing condition. Preprint, 2013,arXiv:1311.1157.Google Scholar
Logan, B. F., Bandlimited functions bounded below over an interval. Notices Amer. Math. Soc. 24 1977, A–331.Google Scholar
Montgomery, H. L., The analytic principle of the large sieve. Bull. Amer. Math. Soc. 84(4) 1978, 547–567.Google Scholar
Plancherel, M. and Pólya, G., Fonctions entières et intégrales de fourier multiples. Comment. Math. Helv. 10(1) 1937, 110–163.Google Scholar
Rosenblum, M. and Rovnyak, J., Topics in Hardy Classes and Univalent Functions (Birkhäuser Advanced Texts: Basler Lehrbücher), Birkhäuser Verlag (Basel, 1994).Google Scholar
Selberg, A., Collected papers. Vol. II. Springer (Berlin, 1991). With a foreword by K. Chandrasekharan.Google Scholar
Stein, E. M., Functions of exponential type. Ann. of Math. (2) 65 1957, 582–592.Google Scholar
Stein, E. M. and Weiss, G., Introduction to Fourier Analysis on Euclidean Spaces (Princeton Mathematical Series 32), Princeton University Press (Princeton, NJ, 1971).Google Scholar
Vaaler, J. D., Some extremal functions in Fourier analysis. Bull. Amer. Math. Soc. (N.S.) 12(2) 1985, 183–216.Google Scholar