Hostname: page-component-cd9895bd7-mkpzs Total loading time: 0 Render date: 2024-12-26T02:41:55.513Z Has data issue: false hasContentIssue false
  • English
  • Français

TILING WITH PUNCTURED INTERVALS

Part of: Designs and configurations Discrete geometry

Published online by Cambridge University Press:  29 October 2018

Harry Metrebian
Harry Metrebian*
Affiliation:
Trinity College Cambridge, CB2 1TQ, U.K. email [email protected]
Get access

Abstract

It was shown by Gruslys, Leader and Tan that any finite subset of 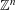$\mathbb{Z}^{n}$ tiles 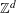$\mathbb{Z}^{d}$ for some 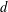$d$. The first non-trivial case is the punctured interval, which consists of the interval 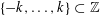$\{-k,\ldots ,k\}\subset \mathbb{Z}$ with its middle point removed: they showed that this tiles 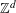$\mathbb{Z}^{d}$ for 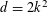$d=2k^{2}$, and they asked if the dimension needed tends to infinity with 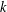$k$. In this note we answer this question: we show that, perhaps surprisingly, every punctured interval tiles 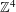$\mathbb{Z}^{4}$.

MSC classification

Primary: 05B45: Tessellation and tiling problems 05B50: Polyominoes 52C22: Tilings in $n$ dimensions
Type
Research Article
Information
Mathematika , Volume 65 , Issue 2 , 2019 , pp. 181 - 189
Copyright
Copyright © University College London 2018 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Adler, A. and Holroyd, F. C., Some results on one-dimensional tilings. Geom. Dedicata 10 1981, 49–58.Google Scholar
Berger, R., The undecidability of the domino problem. Mem. Amer. Math. Soc. 66 1966, 1–72.Google Scholar
Conway, J. H. and Lagarias, J. C., Tiling with polyominoes and combinatorial group theory. J. Combin. Theory Ser. A 53 1990, 183–208.Google Scholar
Dahkle, K., Tiling rectangles with polyominoes. http://eklhad.net/polyomino/index.html (retrieved 7 October 2018).Google Scholar
Friedman, E., Problem of the Month (February 1999).https://www2.stetson.edu/efriedma/mathmagic/0299.html (retrieved 7 October 2018).Google Scholar
Golomb, S. W., Tiling with sets of polyominoes. J. Combin. Theory 9 1970, 60–71.Google Scholar
Gruslys, V., Decomposing the vertex set of a hypercube into isomorphic subgraphs. Preprint, 2016,arXiv:1611.02021.Google Scholar
Gruslys, V., Leader, I. and Tan, T. S., Tiling with arbitrary tiles. Proc. Lond. Math. Soc. (3) 112 2016, 1019–1039.Google Scholar
Gruslys, V., Leader, I. and Tomon, I., Partitioning the Boolean lattice into copies of a poset. J. Combin. Theory Ser. A 161 2019, 81–98.Google Scholar
Gruslys, V. and Letzter, S., Almost partitioning the hypercube into copies of a graph. Preprint, 2016, arXiv:1612.04603.Google Scholar
Kisisel, A. U. O., Polyomino convolutions and tiling problems. J. Combin. Theory Ser. A 95 2001, 373–380.Google Scholar
The Math Forum, Two tiling problems. http://mathforum.org/kb/message.jspa?messageID=6223965(retrieved 7 October 2018).Google Scholar
MathOverflow, Does every polyomino tile $\mathbb{R}^{n}$ for some $n$ ?https://mathoverflow.net/questions/49915/does-every-polyomino-tile-rn-for-some-n (retrieved 7 October 2018).Google Scholar
Tomon, I., Almost tiling of the Boolean lattice with copies of a poset. Electron. J. Combin. 25 2018, #P1.38.Google Scholar