Article contents
SUBGROUPS OF FRACTIONAL DIMENSION IN NILPOTENT OR SOLVABLE LIE GROUPS
Published online by Cambridge University Press: 23 May 2013
Abstract
We construct dense Borel measurable subgroups of Lie groups of intermediate Hausdorff dimension. In particular, we generalize the Erdős–Volkmann construction [Additive Gruppen mit vorgegebener Hausdorffscher Dimension, J. Reine Angew. Math. 221 (1966), 203–208], showing that any nilpotent 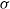 $\sigma $-compact Lie group
$\sigma $-compact Lie group 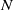 $N$ admits dense Borel subgroups of arbitrary dimension between zero and
$N$ admits dense Borel subgroups of arbitrary dimension between zero and 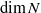 $\dim N$. In algebraic groups defined over a finite extension of the rationals, using diophantine properties of algebraic numbers, we are also able to construct dense subgroups of arbitrary dimension, but the general case remains open. In particular, we raise the following question: does there exist a measurable proper subgroup of
$\dim N$. In algebraic groups defined over a finite extension of the rationals, using diophantine properties of algebraic numbers, we are also able to construct dense subgroups of arbitrary dimension, but the general case remains open. In particular, we raise the following question: does there exist a measurable proper subgroup of 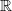 $ \mathbb{R} $ of positive Hausdorff dimension which is stable under multiplication by a transcendental number? Subgroups of nilpotent
$ \mathbb{R} $ of positive Hausdorff dimension which is stable under multiplication by a transcendental number? Subgroups of nilpotent 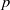 $p$-adic analytic groups are also discussed.
$p$-adic analytic groups are also discussed.
MSC classification
- Type
- Research Article
- Information
- Copyright
- Copyright © University College London 2013
References
- 4
- Cited by


