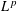Hostname: page-component-cd9895bd7-lnqnp Total loading time: 0 Render date: 2024-12-23T19:01:26.916Z Has data issue: false hasContentIssue false
  • English
  • Français

A SPLITTING PROCEDURE FOR BELLMAN FUNCTIONS AND THE ACTION OF DYADIC MAXIMAL OPERATORS ON $L^{p}$

Part of: Harmonic analysis in several variables Linear function spaces and their duals Stochastic processes

Published online by Cambridge University Press:  19 November 2014

Adam Osękowski
Adam Osękowski*
Affiliation:
Department of Mathematics, Informatics and Mechanics, University of Warsaw, Banacha 2, 02-097 Warsaw, Poland email [email protected]
Get access

Abstract

The purpose of the paper is to introduce a novel “splitting” procedure which can be helpful in the derivation of explicit formulas for various Bellman functions. As an illustration, we study the action of the dyadic maximal operator on 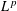$L^{p}$. The associated Bellman function 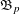$\mathfrak{B}_{p}$, introduced by Nazarov and Treil, was found explicitly by Melas with the use of combinatorial properties of the maximal operator, and was later rediscovered by Slavin, Stokolos and Vasyunin with the use of the corresponding Monge–Ampère partial differential equation. Our new argument enables an alternative simple derivation of 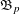$\mathfrak{B}_{p}$.

MSC classification

Primary: 42B25: Maximal functions, Littlewood-Paley theory
Secondary: 46E30: Spaces of measurable functions ($L^p$-spaces, Orlicz spaces, Köthe function spaces, Lorentz spaces, rearrangement invariant spaces, ideal spaces, etc.) 60G42: Martingales with discrete parameter
Type
Research Article
Information
Mathematika , Volume 61 , Issue 1 , January 2015 , pp. 199 - 212
Copyright
Copyright © University College London 2014 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Burkholder, D. L., Boundary value problems and sharp inequalities for martingale transforms. Ann. Probab. 12 1984, 647–702.Google Scholar
Dragičevic, O. and Volberg, A., Bellman function, Littlewood–Paley estimates, and asymptotics of the Ahlfors–Beurling operator in L p(ℂ), p > 1. Indiana Univ. Math. J. 54 2005, 971–995.Google Scholar
Dragičevic, O. and Volberg, A., Bellman function and dimensionless estimates of classical and Ornstein–Uhlenbeck Riesz transforms. J. Operator Theory 56 2006, 167–198.Google Scholar
Melas, A. D., The Bellman functions of dyadic-like maximal operators and related inequalities. Adv. Math. 192 2005, 310–340.CrossRefGoogle Scholar
Melas, A. D., Dyadic-like maximal operators on LlogL functions. J. Funct. Anal. 257 2009, 1631–1654.Google Scholar
Melas, A. D., Sharp general local estimates for dyadic-like maximal operators and related Bellman functions. Adv. Math. 220 2009, 367–426.Google Scholar
Melas, A. D. and Nikolidakis, E. N., On weak-type inequalities for dyadic maximal functions. J. Math. Anal. Appl. 367 2008, 404–410.Google Scholar
Melas, A. D. and Nikolidakis, E. N., Dyadic-like maximal operators on integrable functions and Bellman functions related to Kolmogorov’s inequality. Trans. Amer. Math. Soc. 362 2010, 1571–1597.CrossRefGoogle Scholar
Nazarov, F. and Treil, S., The hunt for Bellman function: applications to estimates of singular integral operators and to other classical problems in harmonic analysis. Algebra i Analiz 8 1997, 32–162.Google Scholar
Nazarov, F., Treil, S. and Volberg, A., The Bellman functions and two-weight inequalities for Haar multipliers. J. Amer. Math. Soc. 12 1999, 909–928.Google Scholar
Nazarov, F., Treil, S. and Volberg, A., Bellman function in stochastic optimal control and harmonic analysis (how our Bellman function got its name). Oper. Theory Adv. Appl. 129 2001, 393–424.Google Scholar
Nikolidakis, E. N., Extremal problems related to maximal dyadic-like operators. J. Math. Anal. Appl. 369 2010, 377–385.Google Scholar
Osękowski, A., Survey article: Bellman function method and sharp inequalities for martingales. Rocky Mountain J. Math. 43 2013, 1759–1823.Google Scholar
Osękowski, A., Weak-type inequalities for maximal operators acting on Lorentz spaces. In Calculus of Variations and PDEs (Banach Center Publications 101) (IMPAN, 2014), 145–162.Google Scholar
Osękowski, A., Sharp L p, ∞→ L q estimates for the dyadic-like maximal operators. J. Fourier Anal. Appl. 20 2014, 911–933.CrossRefGoogle Scholar
Slavin, L., Stokolos, A. and Vasyunin, V., Monge–Ampère equations and Bellman functions: The dyadic maximal operator. C. R. Acad. Sci. Paris, Ser. I 346 2008, 585–588.Google Scholar
Slavin, L. and Vasyunin, V., Sharp results in the integral-form John–Nirenberg inequality. Trans. Amer. Math. Soc. 363 2011, 4135–4169.CrossRefGoogle Scholar
Slavin, L. and Vasyunin, V., Sharp L p estimates on BMO. Indiana Math. J. 61 2012, 1051–1110.Google Scholar
Vasyunin, V., The exact constant in the inverse Hölder inequality for Muckenhoupt weights. Algebra i Analiz 15 2003, 73–117 (Russian); translation in St. Petersburg Math. J., 15 (2004) 49–79.Google Scholar
Vasyunin, V. and Volberg, A., The Bellman function for certain two weight inequality: the case study. St. Petersburg Math. J. 18 2007, 201–222.CrossRefGoogle Scholar
Vasyunin, V. and Volberg, A., Monge–Ampère equation and Bellman optimization of Carleson Embedding Theorems. Amer. Math. Soc. Transl. (2) 226 2009, 195–238.Google Scholar
Vasyunin, V. and Volberg, A., Burkholder’s function via Monge–Ampère equation. Illinois J. Math. 54 2010, 1393–1428.CrossRefGoogle Scholar