Hostname: page-component-586b7cd67f-t8hqh Total loading time: 0 Render date: 2024-11-23T02:55:30.406Z Has data issue: false hasContentIssue false
  • English
  • Français

SARNAK’S SATURATION PROBLEM FOR COMPLETE INTERSECTIONS

Part of: Additive number theory; partitions Diophantine equations

Published online by Cambridge University Press:  24 August 2018

D. Schindler  and
E. Sofos
D. Schindler
Affiliation:
Universiteit Utrecht, Mathematisch Instituut, Budapestlaan 6, Utrecht, 3584 CD, Netherlands email [email protected]
E. Sofos
Affiliation:
Max Planck Institute for Mathematics, Vivatsgasse 7, Bonn, 53111, Germany email [email protected]
Get access

Abstract

We study almost prime solutions of systems of Diophantine equations in the Birch setting. Previous work shows that there exist integer solutions of size 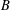$B$ with each component having no prime divisors below 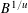$B^{1/u}$, where $u$ equals 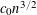$c_{0}n^{3/2}$, $n$ is the number of variables and 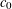$c_{0}$ is a constant depending on the degree and the number of equations. We improve the polynomial growth 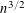$n^{3/2}$ to the logarithmic 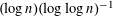$(\log n)(\log \log n)^{-1}$. Our main new ingredients are the generalization of the Brüdern–Fouvry vector sieve in any dimension and the incorporation of smooth weights into the Davenport–Birch version of the circle method.

MSC classification

Primary: 11D72: Equations in many variables
Secondary: 11P32: Goldbach-type theorems; other additive questions involving primes
Type
Research Article
Information
Mathematika , Volume 65 , Issue 1 , 2019 , pp. 1 - 56
Copyright
Copyright © University College London 2018 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Ankeny, N. C. and Onishi, H., The general sieve. Acta Arith. 10(1) 1964/1965, 31–62.Google Scholar
Birch, B. J., Forms in many variables. Proc. R. Soc. Ser. A 265 1961/1962, 245–263.Google Scholar
Blomer, V. and Brüdern, J., A three squares theorem with almost primes. Bull. Lond. Math. Soc. 37(4) 2005, 507–513.Google Scholar
Browning, T. D., Quantitative Arithmetic of Projective Varieties (Progress in Mathematics 277 ), Birkhäuser (Basel, 2009).Google Scholar
Browning, T. D. and Loughran, D. T., Sieving rational points on varieties. Preprint, 2017, arXiv:1705.01999.Google Scholar
Browning, T. D. and Prendiville, S. M., Improvements in Birch’s theorem on forms in many variables. J. Reine Angew. Math. 731 2017, 203–234.Google Scholar
Brüdern, J. and Fouvry, É., Lagrange’s four squares theorem with almost prime variables. J. Reine Angew. Math. 454 1994, 59–96.Google Scholar
Brüdern, J. and Fouvry, É., Le crible à vecteurs. Compos. Math. 102(3) 1996, 337–355.Google Scholar
Buchstab, A. A., Asymptotic estimates of a general number-theoretic function. Mat. Sb. 44(2) 1937, 1239–1246.Google Scholar
Cai, Y., Lagrange’s four squares theorem with variables of special type. Int. J. Number Theory 6(8) 2010, 1801–1817.Google Scholar
Cook, B. and Magyar, Á., Diophantine equations in the primes. Invent. Math. 198(3) 2014, 701–737.Google Scholar
Davenport, H., Cubic forms in 32 variables. Philos. Trans. R. Soc. A 251(A) 1959, 193–232.Google Scholar
Davenport, H., Analytic Methods for Diophantine Equations and Diophantine Inequalities, (Cambridge Mathematical Library), 2nd edn., Cambridge University Press (Cambridge, 2005).Google Scholar
Diamond, H. G. and Halberstam, H., On the sieve parameters 𝛼𝜅 and 𝛽𝜅 for large 𝜅. J. Number Theory 67(1) 1997, 52–84.Google Scholar
Diamond, H. G. and Halberstam, H., A Higher-Dimensional Sieve Method (Cambridge Tracts in Mathematics 177 ), Cambridge University Press (Cambridge, 2008).Google Scholar
Friedlander, J. and Iwaniec, H., Opera de Cribro (American Mathematical Society Colloquium Publications 57 ), American Mathematical Society (Providence, RI, 2010).Google Scholar
Hanselmann, M., Rational points on quartic hypersurfaces. PhD Thesis, Ludwig Maximilians Universität Munchen, 2012.Google Scholar
Heath-Brown, R. and Li, X., Almost prime triples and Chen’s theorem. J. Number Theory 169 2016, 265–294.Google Scholar
Heath-Brown, D. R. and Tolev, D. I., Lagrange’s four squares theorem with one prime and three almost-prime variables. J. Reine Angew. Math. 558 2003, 159–224.Google Scholar
Hooley, C., On nonary cubic forms. J. Reine Angew. Math. 386 1988, 32–98.Google Scholar
Hua, L. K., Some results in the additive prime-number theory. Quart. J. Math. Oxford Ser. (2) 9(1) 1938, 68–80.Google Scholar
van Ittersum, J.-W., Quantitative results on diophantine equations in many variables. Preprint, 2017, arXiv:1709.05126.Google Scholar
van Ittersum, J.-W., Two problems related to the circle method. Master’s Thesis, Universiteit Utrecht, 2017.Google Scholar
Iwaniec, H., Rosser’s sieve. Acta Arith. 36(2) 1980, 171–202.Google Scholar
Jurkat, W. B. and Richert, H.-E., An improvement of Selberg’s sieve method. I. Acta Arith. 11 1965, 217–240.Google Scholar
Klamkin, M. S. and Newman, D. J., Extensions of the Weierstrass product inequalities. Math. Mag. 43 1970, 137–141.Google Scholar
Magyar, Á. and Titichetrakun, T., Almost prime solutions to Diophantine systems of high rank. Int. J. Number Theory 13(6) 2017, 1491–1514.Google Scholar
Montgomery, H. L. and Vaughan, R. C., Multiplicative Number Theory. I. Classical Theory (Cambridge Studies in Advanced Mathematics 97 ), Cambridge University Press (Cambridge, 2007).Google Scholar
Sofos, E. and Wang, Y., Finite saturation for unirational varieties. Int. Math. Res. Not. IMRN 2018, doi:10.1093/imrn/rnx318.Google Scholar
Tolev, D. I., Lagrange’s four squares theorem with variables of special type. In Proceedings of the Session in Analytic Number Theory and Diophantine Equations (Bonner Math. Schriften 360 ), University of Bonn (Bonn, 2003), 17.Google Scholar
Yamagishi, S., Diophantine equations in semiprimes. Preprint, 2017, arXiv:1709.03605.Google Scholar