Hostname: page-component-cd9895bd7-jkksz Total loading time: 0 Render date: 2024-12-23T19:27:37.043Z Has data issue: false hasContentIssue false
  • English
  • Français

The product of n linear forms in a field of series

Published online by Cambridge University Press:  26 February 2010

J. V. Armitage
J. V. Armitage
Affiliation:
67 Haigh Road, Rothwell, Leeds.
Get access

Extract

Let K be a field. We denote by K[t] the integral domain of all polynomials in an indeterminate t with coefficients in K, and by K(t) the quotient field of K[t], i.e. the field of all formal rational functions of t over K. A valuation |f| of the elements f of K(t) can be defined by

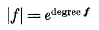
for f ≠ 0, and |0| = 0, where e > 1. This valuation is multiplicative, and has the properties

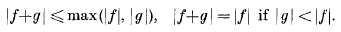
Type
Research Article
Information
Mathematika , Volume 4 , Issue 2 , December 1957 , pp. 132 - 137
Copyright
Copyright © University College London 1957

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

page 132 note † The substance of this paper formed part of the author's Ph.D. thesis (London, 1956).

page 132 note ‡ Mahler, K., Annals of Math., 42 (1941), 488–522.CrossRefGoogle Scholar

page 135 note † See Perron, Algebra I (1st ed.), p. 82, Theorem 75.