Hostname: page-component-cd9895bd7-lnqnp Total loading time: 0 Render date: 2024-12-23T19:30:18.712Z Has data issue: false hasContentIssue false
  • English
  • Français

On the fractional dimension of sets of continued fractions

Part of: Diophantine approximation, transcendental number theory

Published online by Cambridge University Press:  26 February 2010

Tomasz Łuczak
Tomasz Łuczak
Affiliation:
Department of Mathematics, Adam Mickiewicz University, Poznań, Poland.
Get access

Extract

Let [0;a1(ξ), a2(ξ),…] denote the continued fraction expansion of ξ∈[0, 1]. The problem of estimating the fractional dimension of sets of continued fractions emerged in late twenties in papers by Jarnik [6, 7] and Besicovitch [1] and since then has been addressed by a number of authors (see [2, 4, 5, 8, 9]). In particular, Good [4] proved that the set of all ξ, for which an(ξ)→∞ as n→∞ has the Hausdorff dimension ½ For the set of continued fractions whose expansion terms tend to infinity doubly exponentially the dimension decreases even further. More precisely, let

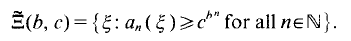
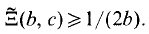Hirst [5] showed that dim On the other hand, Moorthy [8] showed that dim 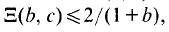where

MSC classification

Secondary: 11J70: Continued fractions and generalizations
Type
Research Article
Information
Mathematika , Volume 44 , Issue 1 , June 1997 , pp. 50 - 53
Copyright
Copyright © University College London 1997

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1.Besicovitch, A. S.. On rational approximation to real numbers. J. London Math. Soc., 9 (1934), 126–131.CrossRefGoogle Scholar
2.Cusick, T. W.. Hausdorff dimension of sets of continued fractions. Quart. J. Math. Oxford, 41 (1990), 277–286.CrossRefGoogle Scholar
3.Falconer, K.. Fractal Geometry (Wiley, Chichester, 1990).Google Scholar
4.Good, I. J.. The fractional dimension theory of continued fractions. Proc. Camb. Phil. Soc., 37 (1941), 199–228.CrossRefGoogle Scholar
5.Hirst, K. E.. A problem in the fractional dimension theory of continued fractions. Quart. J. Math. Oxford, 21 (1970), 29–35.CrossRefGoogle Scholar
6.Jarnik, V.. Zur metrischen Theorie der Diophantischen Approximationen. Prace Mat.-Fiz., 36 (1928), 91–106.Google Scholar
7.Jarnik, V.. Diophantische Approximation und Hausdorffsches Mass. Rec. Math. Soc. Math. Moscou, 36 (1929), 371–382.Google Scholar
8.Moorthy, C. G.. A problem of Good on Hausdorff dimension. Mathematiku, 39 (1992), 244–246.CrossRefGoogle Scholar
9.Rogers, C. A.. Some sets of continued fractions. Proc. London Math. Soc., 14 (1964), 29–44.Google Scholar