Hostname: page-component-cd9895bd7-mkpzs Total loading time: 0 Render date: 2024-12-23T19:06:18.606Z Has data issue: false hasContentIssue false
  • English
  • Français

ON CONFIGURATIONS WHERE THE LOOMIS–WHITNEY INEQUALITY IS NEARLY SHARP AND APPLICATIONS TO THE FURSTENBERG SET PROBLEM

Part of: Discrete geometry Designs and configurations Finite fields and commutative rings (number-theoretic aspects) Extremal combinatorics

Published online by Cambridge University Press:  07 January 2015

Ruixiang Zhang
Ruixiang Zhang*
Affiliation:
Department of Mathematics, Princeton University, Princeton, NJ 08540, U.S.A. email [email protected]
Get access

Abstract

In this paper, we consider the so-called “Furstenberg set problem” in high dimensions. First, following Wolff’s work on the two-dimensional real case, we provide “reasonable” upper bounds for the problem for 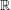$\mathbb{R}$ or 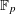$\mathbb{F}_{p}$. Next we study the “critical” case and improve the “trivial” exponent by 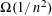${\rm\Omega}(1/n^{2})$ for 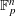$\mathbb{F}_{p}^{n}$. Our key tool in obtaining this lower bound is a theorem about how things behave when the Loomis–Whitney inequality is nearly sharp, as it helps us to reduce the problem to dimension two.

MSC classification

Primary: 11T99: None of the above, but in this section 52C17: Packing and covering in $n$ dimensions
Secondary: 05B25: Finite geometries 05D99: None of the above, but in this section
Type
Research Article
Information
Mathematika , Volume 61 , Issue 1 , January 2015 , pp. 145 - 161
Copyright
Copyright © University College London 2015 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Besicovitch, A. S., Sets of fractional dimensions (iv): on rational approximation to real numbers. J. Lond. Math. Soc. 1(2) 1934, 126–131.CrossRefGoogle Scholar
Bourgain, J., On the Erdős–Volkmann and Katz–Tao ring conjectures. Geom. Funct. Anal. 13(2) 2003, 334–365.Google Scholar
Bourgain, J., Katz, N. and Tao, T., A sum-product estimate in finite fields, and applications. Geom. Funct. Anal. 14(1) 2004, 27–57.CrossRefGoogle Scholar
Dvir, Z., On the size of Kakeya sets in finite fields. J. Amer. Math. Soc. 22(4) 2009, 1093–1097.Google Scholar
Furstenberg, H., Problems in Analysis (Sympos. Salomon Bochner, Princeton Univ., Princeton, NJ, 1969), Princeton University Press (Princeton, NJ, 1970), 41–59.Google Scholar
Guth, L., The polynomial method, fall 2012, project list, http://math.mit.edu/∼lguth/PolyMethod/projlist.pdf.Google Scholar
Katz, N. and Tao, T., Some connections between Falconer’s distance set conjecture and sets of Furstenburg type. New York J. Math. 7 2001, 149–187.Google Scholar
Kuipers, L. and Niederreiter, H., Uniform Distribution of Sequences, Dover Publications (Mineola, NY, 2006).Google Scholar
Tao, T., Edinburgh lecture notes on the Kakeya problem. Preprint, available at http://www.math.ucla.edu/∼tao/preprints/kakeya.html.Google Scholar
Wolff, T., Recent work connected with the Kakeya problem. In Prospects in Mathematics (Princeton, NJ, 1996), American Mathematical Society (Providence, RI, 1999), 129–162.Google Scholar
Wolff, T. H., Lectures on Harmonic Analysis (University Lecture Series 29), American Mathematical Society (Providence, RI, 2003).Google Scholar
Zhang, R., Polynomials with dense zero sets and discrete models of the Kakeya conjecture and the Furstenberg set problem. Preprint, 2014, arXiv:1403.1352.Google Scholar