Hostname: page-component-586b7cd67f-l7hp2 Total loading time: 0 Render date: 2024-11-23T02:39:25.088Z Has data issue: false hasContentIssue false
  • English
  • Français

THE MAXIMAL ORDER OF ITERATED MULTIPLICATIVE FUNCTIONS

Part of: Multiplicative number theory

Published online by Cambridge University Press:  30 July 2019

Christian Elsholtz ,
Marc Technau  and
Niclas Technau
Christian Elsholtz
Affiliation:
Institute of Analysis and Number Theory, Graz University of Technology, Kopernikusgasse 24, 8010 Graz, Austria email [email protected]
Marc Technau
Affiliation:
Institute of Analysis and Number Theory, Graz University of Technology, Kopernikusgasse 24, 8010 Graz, Austria email [email protected]
Niclas Technau
Affiliation:
Raymond and Beverly Sackler School of Mathematical Sciences, Tel Aviv University, 69978 Tel Aviv, Israel email [email protected]
Get access

Abstract

Following Wigert, various authors, including Ramanujan, Gronwall, Erdős, Ivić, Schwarz, Wirsing and Shiu, determined the maximal order of several multiplicative functions, generalizing Wigert’s result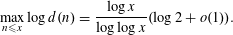

$$\begin{eqnarray}\max _{n\leqslant x}\log d(n)=\frac{\log x}{\log \log x}(\log 2+o(1)).\end{eqnarray}$$
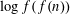On the contrary, for many multiplicative functions, the maximal order of iterations of the functions remains widely open. The case of the iterated divisor function was only solved recently, answering a question of Ramanujan from 1915. Here we determine the maximal order of $\log f(f(n))$ for a class of multiplicative functions 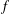$f$. In particular, this class contains functions counting ideals of given norm in the ring of integers of an arbitrary, fixed quadratic number field. As a consequence, we determine such maximal orders for several multiplicative 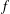$f$ arising as a normalized function counting representations by certain binary quadratic forms. Incidentally, for the non-multiplicative function 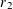$r_{2}$ which counts how often a positive integer is represented as a sum of two squares, this entails the asymptotic formula
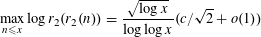$$\begin{eqnarray}\max _{n\leqslant x}\log r_{2}(r_{2}(n))=\frac{\sqrt{\log x}}{\log \log x}(c/\sqrt{2}+o(1))\end{eqnarray}$$
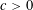 with some explicitly given constant $c>0$.

MSC classification

Primary: 11N37: Asymptotic results on arithmetic functions
Type
Research Article
Information
Mathematika , Volume 65 , Issue 4 , 2019 , pp. 990 - 1009
Copyright
Copyright © University College London 2019 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

The third author was supported, while working on this paper, by the Austrian Science Fund (FWF): by either Project W1230 Doctoral Program “Discrete Mathematics” or Project Y-901.

References

Andrews, G. E. and Berndt, B., Ramanujan’s Lost Notebook. Part III (Highly Composite Numbers), Springer (New York, 2012), 359–402.10.1007/978-1-4614-3810-6_10Google Scholar
Babanazarov, B. and Podzharskij, Ya. I., On the maximal order of arithmetic functions. Izv. Akad. Nauk UzSSR Ser. Fiz.-Mat. Nauk 1987(1) 1987, 18–23, and p. 93.Google Scholar
Bayless, J., The Lucas–Pratt primality tree. Math. Comput. 77 2008, 495–502.10.1090/S0025-5718-07-02002-9Google Scholar
Buttkewitz, Y., Elsholtz, C., Ford, K. and Schlage-Puchta, J.-C., A problem of Ramanujan, Erdős, and Kátai on the iterated divisor function. Int. Math. Res. Not. IMRN 2012(17) 2012, 4051–4061.10.1093/imrn/rnr175Google Scholar
Drozdova, A. A. and Freĭman, G. A., The estimation of certain arithmetic functions. Elabuž. Gos. Ped. Inst. Učen. Zap. 3 1958, 160–165.Google Scholar
Erdős, P. and Ivić, A., On the iterates of the enumerating function of finite abelian groups. Bull. Acad. Serbe Sci. Arts Cl. Sci. Math. Natur. No. 17 1989, 13–22.Google Scholar
Erdős, P. and Kátai, I., On the growth of d k(n). Fibonacci Quart. 7 1969, 267–274.Google Scholar
Ford, K., The distribution of totients. Ramanujan J. 2(1–2) 1998, 67–151.10.1023/A:1009761909132Google Scholar
Gronwall, T. H., Some asymptotic expressions in the theory of numbers. Trans. Amer. Math. Soc. 14(1) 1913, 113–122.10.1090/S0002-9947-1913-1500940-6Google Scholar
Hardy, G. H. and Wright, E. M., An Introduction to the Theory of Numbers, Clarendon Press (Oxford, 1954).Google Scholar
Heppner, E., Die maximale Ordnung primzahl-unabhängiger multiplikativer Funktionen. Arch. Math. (Basel) 24 1973, 63–66.10.1007/BF01228175Google Scholar
Hilberdink, T., Maximal order of a class of multiplicative functions. Ann. Univ. Sci. Budapest. Sect. Comput. 43 2014, 217–237.Google Scholar
Ireland, K. and Rosen, M., A Classical Introduction to Modern Number Theory, 2nd edn., Springer (New York, 1990).10.1007/978-1-4757-2103-4Google Scholar
Ivić, A., On the maximal order of certain arithmetic functions. Filomat 9(3) 1995, 483–492.Google Scholar
Iwaniec, H. and Kowalski, E., Analytic Number Theory, American Mathematical Society (AMS) (Providence, RI, 2004).Google Scholar
Knopfmacher, J., A prime-divisor function. Proc. Amer. Math. Soc. 40 1973, 373–377.10.1090/S0002-9939-1973-0327694-7Google Scholar
Knopfmacher, J., Arithmetical properties of finite rings and algebras, and analytic number theory. VI. Maximum orders of magnitude. J. Reine Angew. Math. 277 1975, 45–62.Google Scholar
Krätzel, E., Die maximale Ordnung der Anzahl der wesentlich verschiedenen abelschen Gruppen n-ter Ordnung. Quart. J. Math. Oxford Ser. (2) 21 1970, 273–275.Google Scholar
Luca, F. and Pomerance, C., On the range of the iterated Euler function. In Combinatorial Number Theory, de Gruyter (Berlin, 2009), 101–116.Google Scholar
Maier, H., On the third iterates of the 𝜑- and 𝜎-functions. Colloq. Math. 49(1) 1984, 123–130.10.4064/cm-49-1-123-130Google Scholar
Mąkowski, A., On two conjectures of Schinzel. Elem. Math. 31(6) 1976, 140–141.Google Scholar
Nicolas, J.-L., Grandes valeurs d’une certaine classe de fonctions arithmétiques. Stud. Sci. Math. Hungar. 15(1–3) 1980, 71–77.Google Scholar
Nicolas, J.-L., On highly composite numbers. In Ramanujan Revisited: Proceedings of the Centenary Conference, Academic Press (Boston, MA, 1988), 215–244.Google Scholar
Norton, K. K., Upper bounds for sums of powers of divisor functions. J. Number Theory 40(1) 1992, 60–85.10.1016/0022-314X(92)90028-NGoogle Scholar
Postnikov, A. G., Introduction to Analytic Number Theory (Translations of Mathematical Monographs 68 ), American Mathematical Society (Providence, RI, 1988).10.1090/mmono/068Google Scholar
Ramanujan, S., The Lost Notebook and Other Unpublished Papers, Springer (Berlin, 1988).Google Scholar
Ramanujan, S., Highly composite numbers. Ramanujan J. 1(2) 1997, 119–153. Annotated and with a foreword by Jean-Louis Nicolas and Guy Robin.Google Scholar
Ramanujan, S., Highly composite numbers [Proc. London Math. Soc. (2) 14 (1915), 347–409]. In Collected Papers of Srinivasa Ramanujan, AMS Chelsea (Providence, RI, 2000), 78–128.Google Scholar
Schinzel, A., Ungelöste Probleme. Elem. Math. 14 1959, 60–61.Google Scholar
Shiu, P., The maximum orders of multiplicative functions. Quart. J. Math. Oxford Ser. (2) 31(122) 1980, 247–252.10.1093/qmath/31.2.247Google Scholar
Smati, A., Sur un problème de S. Ramanujan. C. R. Math. Acad. Sci. Paris 340(1) 2005, 1–4.10.1016/j.crma.2004.11.014Google Scholar
Smati, A., Sur un problème d’Erdős et Kátai. Ann. Univ. Sci. Budapest. Sect. Comput. 29 2008, 213–238.Google Scholar
Suryanarayana, D. and Sitaramachandra Rao, R., On the true maximum order of a class of arithmetical functions. Math. J. Okayama Univ. 17(2) 1975, 95–101.Google Scholar
Wigert, S., Sur l’ordre de grandeur du nombre des diviseurs d’un entier. Ark. Mat. 3(18) 1907, 1–9.Google Scholar