Hostname: page-component-586b7cd67f-vdxz6 Total loading time: 0 Render date: 2024-11-26T14:01:08.107Z Has data issue: false hasContentIssue false
  • English
  • Français

HOMOGENIZATION OF THE SYSTEM OF HIGH-CONTRAST MAXWELL EQUATIONS

Part of: Partial differential operators Elliptic equations and systems

Published online by Cambridge University Press:  27 February 2015

Kirill Cherednichenko  and
Shane Cooper
Kirill Cherednichenko
Affiliation:
Department of Mathematical Sciences, University of Bath, Claverton Down, Bath BA2 7AY, U.K. email [email protected]
Shane Cooper
Affiliation:
Laboratoire de Mécanique et Génie Civil de Montpellier, 860 Rue de Saint-Priest, 34095 Montpellier, France email [email protected]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We study the system of Maxwell equations for a periodic composite dielectric medium with components whose dielectric permittivities ${\it\epsilon}$ have a high degree of contrast between each other. We assume that the ratio between the permittivities of the components with low and high values of ${\it\epsilon}$ is of the order 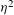${\it\eta}^{2}$, where 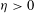${\it\eta}>0$ is the period of the medium. We determine the asymptotic behaviour of the electromagnetic response of such a medium in the “homogenization limit”, as 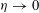${\it\eta}\rightarrow 0$, and derive the limit system of Maxwell equations in 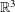$\mathbb{R}^{3}$. Our results extend a number of conclusions of a paper by Zhikov [On gaps in the spectrum of some divergent elliptic operators with periodic coefficients. St. Petersburg Math. J.16(5) (2004), 719–773] to the case of the full system of Maxwell equations.

MSC classification

Primary: 35J15: Second-order elliptic equations 35J70: Degenerate elliptic equations 47F05: Partial differential operators (should also be assigned at least one other classification number in section 47)
Type
Research Article
Information
Mathematika , Volume 61 , Issue 2 , May 2015 , pp. 475 - 500
Creative Commons
Creative Common License - CCCreative Common License - BY
This article is distributed with Open Access under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted reuse, distribution, and reproduction in any medium, provided that the original work is properly cited.
Copyright
Copyright © University College London 2015

References

Adams, R. A., Sobolev Spaces, Academic Press (New York–San Francisco–London, 1975).Google Scholar
Allaire, G., Homogenization and two-scale convergence. SIAM J. Math. Anal. 23 1992, 1482–1518.CrossRefGoogle Scholar
Bensoussan, A., Lions, J.-L. and Papanicolaou, G. C., Asymptotic Analysis for Periodic Structures, North-Holland (1978).Google Scholar
Berkolaiko, G. and Kuchment, P., Introduction to Quantum Graphs (Mathematical Surveys and Monographs 186), American Mathematical Society (Providence, RI, 2013).Google Scholar
Cherednichenko, K. D., Two-scale asymptotics for non-local effects in composites with highly anisotropic fibres. Asymptot. Anal. 49 2006, 39–59.Google Scholar
Cherednichenko, K. D. and Cooper, S., Resolvent estimates for high-contrast elliptic problems with periodic coefficients, submitted (2013).Google Scholar
Cherednichenko, K. D., Cooper, S. and Guenneau, S., Spectral analysis of one-dimensional high-contrast elliptic problems with periodic coefficients. Multiscale Model. Simul. 13 2015, 72–98.CrossRefGoogle Scholar
Cioranescu, D., Damlamian, A. and Griso, G., Periodic unfolding and homogenisation. C. R. Math. Acad. Sci. Paris 335(1) 2002, 99–104.CrossRefGoogle Scholar
Cooper, S., Two-scale homogenisation of partially degenerating PDEs with applications to photonic crystals and elasticity. PhD Thesis, University of Bath, 2012.Google Scholar
Dautray, R. and Lions, J.-L., Mathematical Analysis and Numerical Methods for Science and Technology, Vol. 3 (Spectral Theory and Applications), Springer (Berlin, 1990).Google Scholar
Evans, L., Partial Differential Equations (Graduate Studies in Mathematics 19), American Mathematical Society (Providence, RI, 2010).Google Scholar
Figotin, A. and Kuchment, P., Spectral properties of classical waves in high-contrast periodic media. SIAM J. Appl. Math. 58 1998, 683–702.CrossRefGoogle Scholar
Hempel, R. and Lienau, K., Spectral properties of periodic media in the large coupling limit. Comm. Partial Differential Equations 25 2000, 1445–1470.CrossRefGoogle Scholar
Jikov, V. V., Kozlov, S. M. and Oleinik, O. A., Homogenization of Differential Operators and Integral Functionals, Springer (1994).CrossRefGoogle Scholar
Joannopoulos, J. D., Meade, R. D. and Winn, J. N., Photonic Crystals: Molding the Flow of Light, Princeton University Press (Princeton, NJ, 1995).Google Scholar
Kamotski, I. V. and Smyshlyaev, V. P., 2006, Localised modes due to defects in high contrast periodic media via homogenisation. BICS preprint 3/06, 2006, available online at: http://www.bath.ac.uk/mathsci/bics/preprints/bics063.pdf.Google Scholar
Kamotski, I. V. and Smyshlyaev, V. P., Two-scale homogenization for a class of partially degenerating PDE systems. Preprint, 2013, arXiv:1309.4579v1.Google Scholar
Kozlov, V. A., Maz’ya, V. G. and Movchan, A. B., Asymptotic Analysis of Fields in Multi-Structures, Oxford University Press (Oxford, 1999).CrossRefGoogle Scholar
Kuchment, P., Floquet Theory for Partial Differential Equations (Operator Theory: Advances and Applications 60), Birkhäuser (Basel, 1993).CrossRefGoogle Scholar
Maz’ya, V. G., Sobolev Spaces, Springer (Berlin–Tokyo, 1985).CrossRefGoogle Scholar
Maz’ya, V. G., Nazarov, S. A. and Plamenevskii, B. A., Asymptotic Theory of Elliptic Boundary Value Problems in Singularly Perturbed Domains, Vol. II (Operator Theory: Advances and Applications 112), Birkhäuser (Basel, 2000).Google Scholar
Nguetseng, G., A general convergence result for a functional related to the theory of homogenization. SIAM J. Math. Anal. 20(3) 1989, 608–623.CrossRefGoogle Scholar
Parnovski, L., Bethe–Sommerfeld conjecture. Ann. Henri Poincaré 9(3) 2008, 457–508.CrossRefGoogle Scholar
Pastukhova, S. E., Asymptotic analysis of elasticity problems on thin periodic structures. Netw. Heterog. Media 4(3) 2009, 577–604.CrossRefGoogle Scholar
Russell, P., Photonic crystal fibers. Science 299 2003, 358–362.CrossRefGoogle ScholarPubMed
Sandrakov, G. V., Averaging of non-stationary equations with contrast coefficients. Dokl. Akad. Nauk 355(5) 1997, 605–608.Google Scholar
Stein, E. M., Singular Integrals and Differentiability Properties of Functions, Princeton University Press (Princeton, NJ, 1970).Google Scholar
Zhikov, V. V., On an extension of the method of two-scale convergence and its applications. Sb. Math. 191(7) 2000, 973–1014.CrossRefGoogle Scholar
Zhikov, V. V., On gaps in the spectrum of some divergent elliptic operators with periodic coefficients. St. Petersburg Math. J. 16(5) 2004, 719–773.Google Scholar