Hostname: page-component-78c5997874-t5tsf Total loading time: 0 Render date: 2024-11-06T00:25:53.105Z Has data issue: false hasContentIssue false
  • English
  • Français

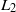HOMOGENIZATION OF THE DIRICHLET PROBLEM FOR ELLIPTIC SYSTEMS: $L_2$-OPERATOR ERROR ESTIMATES

Part of: Partial differential equations

Published online by Cambridge University Press:  01 February 2013

T. A. Suslina
T. A. Suslina*
Affiliation:
Department of Physics, St. Petersburg State University, Ul’yanovskaya 3, Petrodvorets, St. Petersburg, 198504, Russia (email: [email protected])
Get access

Abstract

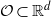Let $\mathcal {O} \subset \mathbb {R}^d$ be a bounded domain of class 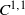$C^{1,1}$. In the Hilbert space 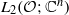$L_2(\mathcal {O};\mathbb {C}^n)$, we consider a matrix elliptic second order differential operator $\mathcal {A}_{D,\varepsilon }$ with the Dirichlet boundary condition. Here 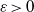$\varepsilon \gt 0$ is the small parameter. The coefficients of the operator are periodic and depend on 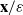$\mathbf {x}/\varepsilon $. There are no regularity assumptions on the coefficients. A sharp order operator error estimate 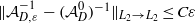$\|\mathcal {A}_{D,\varepsilon }^{-1} - (\mathcal {A}_D^0)^{-1} \|_{L_2 \to L_2} \leq C \varepsilon $ is obtained. Here 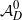$\mathcal {A}^0_D$is the effective operator with constant coefficients and with the Dirichlet boundary condition.

MSC classification

Secondary: 35B27: Homogenization; equations in media with periodic structure
Type
Research Article
Information
Mathematika , Volume 59 , Issue 2 , July 2013 , pp. 463 - 476
Copyright
Copyright © 2013 University College London 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

[1]Bakhvalov, N. S. and Panasenko, G. P., Homogenization: averaging processes in periodic media. In Mathematical Problems in Mechanics of Composite Materials, Nauka (Moscow, 1984); English transl., Math. Appl. (Soviet Ser.), Vol. 36, Kluwer Academic Publishing Group (Dordrecht, 1989).Google Scholar
[2]Bensoussan, A., Lions, J.-L. and Papanicolaou, G., Asymptotic Analysis for Periodic Structures (Studies in Mathematics and its Applications 5), North-Holland Publishing Co. (Amsterdam–New York, 1978).Google Scholar
[3]Birman, M. Sh. and Suslina, T. A., Threshold effects near the lower edge of the spectrum for periodic differential operators of mathematical physics. In Systems, Approximation, Singular Integral Operators, and Related Topics (Bordeaux, 2000) (Operator Theory: Advances and Applications 129), Birkhäuser (Basel, 2001), 71–107.CrossRefGoogle Scholar
[4]Birman, M. Sh. and Suslina, T. A., Second order periodic differential operators. Threshold properties and homogenization. Algebra i Analiz 15(5) (2003), 1–108; English transl., St. Petersburg Math. J. 15(5) (2004), 639–714.Google Scholar
[5]Birman, M. Sh. and Suslina, T. A., Homogenization with corrector term for periodic elliptic differential operators. Algebra i Analiz 17(6) (2005), 1–104; English transl., St. Petersburg Math. J. 17(6) (2006), 897–973.Google Scholar
[6]Birman, M. Sh. and Suslina, T. A., Homogenization with corrector term for periodic differential operators. Approximation of solutions in the Sobolev class $H^1(\mathbb {R}^d)$. Algebra i Analiz 18(6) (2006), 1–130; English transl., St. Petersburg Math. J. 18(6) (2007), 857–955.Google Scholar
[7]Griso, G., Error estimate and unfolding for periodic homogenization. Asymptot. Anal. 40 (2004), 269–286.Google Scholar
[8]Griso, G., Interior error estimate for periodic homogenization. Anal. Appl. 4(1) (2006), 61–79.CrossRefGoogle Scholar
[9]Kenig, C. E., Lin, F. and Shen, Z., Convergence rates in $L^2$ for elliptic homogenization problems. Arch. Ration. Mech. Anal. 203(3) (2012), 1009–1036.CrossRefGoogle Scholar
[10]McLean, W., Strongly Elliptic Systems and Boundary Integral Equations, Cambridge University Press (Cambridge, 2000).Google Scholar
[11]Pakhnin, M. A. and Suslina, T. A., Homogenization of the elliptic Dirichlet problem: error estimates in the $(L_2 \to H^1)$-norm. Funktsional. Anal. i Prilozhen. 46(2) (2012), 92–96; English transl.,Funct. Anal. Appl. 46(2), (2012), 155-159.CrossRefGoogle Scholar
[12]Pakhnin, M. A. and Suslina, T. A., Operator error estimates for homogenization of the elliptic Dirichlet problem in a bounded domain. Algebra i Analiz 24(6) (2012), 139–177; English transl., St. Petersburg Math. J. 24(6) (2013) (to appear).Google Scholar
[13]Pastukhova, S. E., On some estimates in homogenization problems of elasticity theory. Dokl. Akad. Nauk 406(5) (2006), 604–608; English transl., Dokl. Math. 73 (2006), 102–106.Google Scholar
[14]Zhikov, V. V., On the operator estimates in the homogenization theory. Dokl. Akad. Nauk 403(3) (2005), 305–308; English transl., Dokl. Math. 72 (2005), 535–538.Google Scholar
[15]Zhikov, V. V., On some estimates of homogenization theory. Dokl. Akad. Nauk 406(5) (2006), 597–601; English transl., Dokl. Math. 73 (2006), 96–99.Google Scholar
[16]Zhikov, V. V., Kozlov, S. M. and Olejnik, O. A., Homogenization of Differential Operators, Nauka (Moscow, 1993); English transl., Springer (Berlin, 1994).Google Scholar
[17]Zhikov, V. V. and Pastukhova, S. E., On operator estimates for some problems in homogenization theory. Russ. J. Math. Phys. 12(4) (2005), 515–524.Google Scholar