Hostname: page-component-586b7cd67f-t8hqh Total loading time: 0 Render date: 2024-11-23T03:03:02.662Z Has data issue: false hasContentIssue false
  • English
  • Français

GOLDBACH REPRESENTATIONS IN ARITHMETIC PROGRESSIONS AND ZEROS OF DIRICHLET L-FUNCTIONS

Part of: Additive number theory; partitions Zeta and $L$-functions: analytic theory

Published online by Cambridge University Press:  24 August 2018

Gautami Bhowmik ,
Karin Halupczok ,
Kohji Matsumoto  and
Yuta Suzuki
Gautami Bhowmik
Affiliation:
Laboratoire Paul Painlevé, Labex-Cempi, Université Lille 1, 59655 Villeneuve d’Ascq Cedex, France email [email protected]
Karin Halupczok
Affiliation:
Mathematisch-Naturwissenschaftliche Fakultät, Heinrich-Heine-Universität Düsseldorf, Universitätsstr. 1, 40225 Düsseldorf, Germany email [email protected]
Kohji Matsumoto
Affiliation:
Graduate School of Mathematics, Nagoya University, Furocho, Chikusa-ku, Nagoya 464-8602, Japan email [email protected]
Yuta Suzuki
Affiliation:
Graduate School of Mathematics, Nagoya University, Furocho, Chikusa-ku, Nagoya 464-8602, Japan email [email protected]
Get access

Abstract

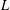Assuming a conjecture on distinct zeros of Dirichlet $L$-functions we get asymptotic results on the average number of representations of an integer as the sum of two primes in arithmetic progression. On the other hand the existence of good error terms gives information on the location of zeros of 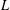$L$-functions. Similar results are obtained for an integer in a congruence class expressed as the sum of two primes.

MSC classification

Primary: 11P32: Goldbach-type theorems; other additive questions involving primes 11M26: Nonreal zeros of $zeta (s)$ and $L(s, chi)$; Riemann and other hypotheses
Secondary: 11M41: Other Dirichlet series and zeta functions
Type
Research Article
Information
Mathematika , Volume 65 , Issue 1 , 2019 , pp. 57 - 97
Copyright
Copyright © University College London 2018 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

The fourth author is supported by Grant-in-Aid for JSPS Research Fellow (Grant Number: JP16J00906) and had the partial aid of CEMPI for his stay at Lille.

References

Bauer, C., Goldbach’s conjecture in arithmetic progressions: number and size of exceptional prime moduli. Arch. Math. 108 2016, 159–172.Google Scholar
Bhowmik, G. and Ruzsa, I. Z., Average Goldbach and the Quasi-Riemann hypothesis. Anal. Math. 44(1) 2018, 51–56.Google Scholar
Bhowmik, G. and Schlage-Puchta, J.-C., Mean representation number of integers as the sum of primes. Nagoya Math. J. 200 2010, 27–33.Google Scholar
Bhowmik, G. and Schlage-Puchta, J.-C., Meromorphic continuation of the Goldbach generating function. Funct. Approx. Comment. Math. 45 2011, 43–53.Google Scholar
Conrey, J. B., The Riemann hypothesis. Notices Amer. Math. Soc. 50 2003, 341–353.Google Scholar
Egami, S. and Matsumoto, K., Convolutions of the von Mangoldt function and related Dirichlet series. In Number Theory. Sailing on the Sea of Number Theory (Series on Number Theory and its Applications 2 ) (eds Kanemitsu, S. and Liu, J.-Y.), World Scientific (2007), 1–23.Google Scholar
Ford, K., Soundararajan, K. and Zaharescu, A., On the distribution of imaginary parts of zeros of the Riemann zeta function II. Math. Ann. 343 2009, 487–505.Google Scholar
Fujii, A., An additive problem of prime numbers. Acta Arith. 58 1991, 173–179.Google Scholar
Gallagher, P. X., A large sieve density estimate near 𝜎 = 1. Invent. Math. 11 1970, 329–339.Google Scholar
Gonek, S. M., An explicit formula of Landau and its applications to the theory of the zeta-function. Contemp. Math. 143 1993, 395–413.Google Scholar
Granville, A., Refinements of Goldbach’s conjecture, and the generalized Riemann hypothesis. Funct. Approx. Comment. Math. 37 2007, 159–173; Corrigendum, ibid. 38 (2008), 235–237.Google Scholar
Hardy, G. H. and Littlewood, J. E., Some problems of ‘Partitio Numerorum’; III: On the expression of a number as a sum of primes. Acta Math. 44 1923, 1–70.Google Scholar
Liu, M.-C. and Zhan, T., The Goldbach problem with primes in arithmetic progressions. In Analytic Number Theory (London Mathematical Society Lecture Note Series 247 ) (ed. Motohashi, Y.), Cambridge University Press (Cambridge, 1997), 227–251.Google Scholar
Montgomery, H. L., Ten Lectures on the Interface Between Analytic Number Theory and Harmonic Analysis (Conference Board of the Mathematical Sciences 84 ), American Mathematical Society (Providence, RI, 1994).Google Scholar
Montgomery, H. L. and Vaughan, R. C., Multiplicative Number Theory I. Classical Theory, Cambridge University Press (Cambridge, 2007).Google Scholar
Rüppel, F., Convolutions of the von Mangoldt function over residue classes. Šiauliai Math. Semin. 7(15) 2012, 135–156.Google Scholar
Suzuki, Y., A mean value of the representation function for the sum of two primes in arithmetic progressions. Int. J. Number Theory 13(4) 2017, 977–990.Google Scholar