We study the geometry of the space of measures of a compact ultrametric space 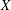$X$, endowed with the 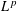$L^{p}$ Wasserstein distance from optimal transportation. We show that the power 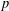$p$ of this distance makes this Wasserstein space affinely isometric to a convex subset of 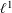$\ell ^{1}$. As a consequence, it is connected by 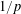$1/p$-Hölder arcs, but any ${\it\alpha}$-Hölder arc with 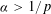${\it\alpha}>1/p$ must be constant. This result is obtained via a reformulation of the distance between two measures which is very specific to the case when 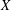$X$ is ultrametric; however, thanks to the Mendel–Naor ultrametric skeleton it has consequences even when 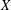$X$ is a general compact metric space. More precisely, we use it to estimate the size of Wasserstein spaces, measured by an analogue of Hausdorff dimension that is adapted to (some) infinite-dimensional spaces. The result we get generalizes greatly our previous estimate, which needed a strong rectifiability assumption. The proof of this estimate involves a structural theorem of independent interest: every ultrametric space contains large co-Lipschitz images of regular ultrametric spaces, i.e. spaces of the form 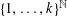$\{1,\dots ,k\}^{\mathbb{N}}$ with a natural ultrametric. We are also led to an example of independent interest: a space of positive lower Minkowski dimension, all of whose proper closed subsets have vanishing lower Minkowski dimension.