Introduction. This paper describes a natural way to associate fractal setsto a certain class of absolutely convergent series in 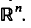In Theorem 1 we give sufficient conditions for such series. Theorem 2 shows that each analytic function gives a different fractal series for each number in a certain open set. Theorem 3 gives the Hausdorff dimension of the associated sets to fractal series, under suitable conditions on the series. This theorem can be applied to some standard series in analysis, such as the binomial, exponential and trigonometrical complex series. The associated sets to geometrical complex series are selfsimilar sets previously studied by M. F. Barnsley from a different (dynamical) point of view (see refs. [5], [6]).