Article contents
FLAG AREA MEASURES
Published online by Cambridge University Press: 23 July 2019
Abstract
A flag area measure on an  $n$-dimensional euclidean vector space is a continuous translation-invariant valuation with values in the space of signed measures on the flag manifold consisting of a unit vector
$n$-dimensional euclidean vector space is a continuous translation-invariant valuation with values in the space of signed measures on the flag manifold consisting of a unit vector 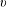 $v$ and a
$v$ and a 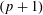 $(p+1)$-dimensional linear subspace containing
$(p+1)$-dimensional linear subspace containing 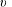 $v$ with
$v$ with 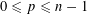 $0\leqslant p\leqslant n-1$. Using local parallel sets, Hinderer constructed examples of
$0\leqslant p\leqslant n-1$. Using local parallel sets, Hinderer constructed examples of 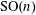 $\text{SO}(n)$-covariant flag area measures. There is an explicit formula for his flag area measures evaluated on polytopes, which involves the squared cosine of the angle between two subspaces. We construct a more general sequence of smooth
$\text{SO}(n)$-covariant flag area measures. There is an explicit formula for his flag area measures evaluated on polytopes, which involves the squared cosine of the angle between two subspaces. We construct a more general sequence of smooth 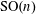 $\text{SO}(n)$-covariant flag area measures via integration over the normal cycle of appropriate differential forms. We provide an explicit description of our measures on polytopes, which involves an arbitrary elementary symmetric polynomial in the squared cosines of the principal angles between two subspaces. Moreover, we show that these flag area measures span the space of all smooth
$\text{SO}(n)$-covariant flag area measures via integration over the normal cycle of appropriate differential forms. We provide an explicit description of our measures on polytopes, which involves an arbitrary elementary symmetric polynomial in the squared cosines of the principal angles between two subspaces. Moreover, we show that these flag area measures span the space of all smooth 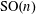 $\text{SO}(n)$-covariant flag area measures, which gives a classification result in the spirit of Hadwiger’s theorem.
$\text{SO}(n)$-covariant flag area measures, which gives a classification result in the spirit of Hadwiger’s theorem.
MSC classification
- Type
- Research Article
- Information
- Copyright
- Copyright © University College London 2019
References
- 1
- Cited by


