Hostname: page-component-cd9895bd7-mkpzs Total loading time: 0 Render date: 2024-12-23T18:50:51.307Z Has data issue: false hasContentIssue false
  • English
  • Français

DOUBLE-NORMAL PAIRS IN SPACE

Part of: Discrete geometry

Published online by Cambridge University Press:  14 August 2014

János Pach  and
Konrad J. Swanepoel
János Pach
Affiliation:
EPFL Lausanne, Switzerland Rényi Institute, Budapest, Hungary email [email protected]
Konrad J. Swanepoel
Affiliation:
Department of Mathematics, London School of Economics and Political Science, Houghton Street, London WC2A 2AE, U.K. email [email protected]
Get access

Abstract

A double-normal pair of a finite set 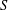$S$ of points that spans 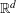$\mathbb{R}^{d}$ is a pair of points 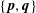$\{\mathbf{p},\mathbf{q}\}$ from 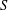$S$ such that 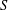$S$ lies in the closed strip bounded by the hyperplanes through 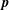$\mathbf{p}$ and 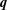$\mathbf{q}$ perpendicular to 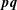$\mathbf{p}\mathbf{q}$. A double-normal pair 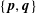$\{\mathbf{p},\mathbf{q}\}$ is strict if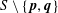$S\setminus \{\mathbf{p},\mathbf{q}\}$ lies in the open strip. The problem of estimating the maximum number 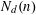$N_{d}(n)$ of double-normal pairs in a set of $n$ points in 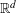$\mathbb{R}^{d}$, was initiated by Martini and Soltan [Discrete Math. 290 (2005), 221–228]. It was shown in a companion paper that in the plane, this maximum is 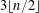$3\lfloor n/2\rfloor$, for every 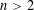$n>2$. For 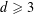$d\geqslant 3$, it follows from the Erdős–Stone theorem in extremal graph theory that 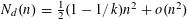$N_{d}(n)=\frac{1}{2}(1-1/k)n^{2}+o(n^{2})$ for a suitable positive integer 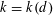$k=k(d)$. Here we prove that 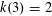$k(3)=2$ and, in general, 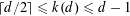$\lceil d/2\rceil \leqslant k(d)\leqslant d-1$. Moreover, asymptotically we have 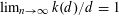$\lim _{n\rightarrow \infty }k(d)/d=1$. The same bounds hold for the maximum number of strict double-normal pairs.

MSC classification

Primary: 52C10: Erdős problems and related topics of discrete geometry
Type
Research Article
Information
Mathematika , Volume 61 , Issue 1 , January 2015 , pp. 259 - 272
Copyright
Copyright © University College London 2014 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Erdős, P., On sets of distances of n points in Euclidean space. Magyar Tud. Akad. Mat. Kut. Int. Közl. 5 1960, 165–169.Google Scholar
Erdős, P. and Füredi, Z., The greatest angle among n points in the d-dimensional Euclidean space. (North-Holland Mathematics Studies 75), North-Holland (Amsterdam, 1983), 275–283.Google Scholar
Erdős, P. and Stone, A. H., On the structure of linear graphs. Bull. Amer. Math. Soc. (N.S.) 52 1946, 1087–1091.Google Scholar
Grünbaum, B., A proof of Vázsonyi’s conjecture. Bull. Res. Council Israel, Section A 6 1956, 77–78.Google Scholar
Heppes, A., Beweis einer Vermutung von A. Vázsonyi. Acta Math. Acad. Sci. Hungar. 7 1956, 463–466.CrossRefGoogle Scholar
Kupavskii, A., Diameter graphs in ℝ4. Discrete Comput. Geom. 51 2014, 842–858.Google Scholar
Makai, E. Jr. and Martini, H., On the number of antipodal or strictly antipodal pairs of points in finite subsets of ℝd. In Applied Geometry and Discrete Mathematics (DIMACS Series in Discrete Mathematics and Theoretical Computer Science 4), American Mathematical Society (Providence, RI, 1991), 457–470.Google Scholar
Makai, E. Jr. and Martini, H., On the number of antipodal or strictly antipodal pairs of points in finite subsets of ℝd. II. Period. Math. Hungar. 27 1993, 185–198.Google Scholar
Makai, E. Jr., Martini, H., Nguên, H., Soltan, V. and Talata, I., On the number of antipodal or strictly antipodal pairs of points in finite subsets of $\mathbb{R}^{d}$. III. Manuscript.Google Scholar
Martini, H. and Soltan, V., Antipodality properties of finite sets in Euclidean space. Discrete Math. 290 2005, 221–228.Google Scholar
Pach, J., A remark on transversal numbers. In The Mathematics of Paul Erdős II (Algorithms and Combinatorics 14) (ed. Graham, R. L. et al. ), Springer (Berlin, 1997), 310–317.Google Scholar
Pach, J. and Swanepoel, K. J., Double-normal pairs in the plane and on the sphere. Beitr. Algebra Geom., to appear, arXiv:1404.2624.Google Scholar
Straszewicz, S., Sur un problème géométrique de P. Erdős. Bull. Acad. Polon. Sci. Cl. III. 5 1957, 39–40, IV–V.Google Scholar
Swanepoel, K. J., Unit distances and diameters in Euclidean spaces. Discrete Comput. Geom. 41 2009, 1–27.CrossRefGoogle Scholar