Hostname: page-component-cd9895bd7-dk4vv Total loading time: 0 Render date: 2024-12-23T19:00:38.264Z Has data issue: false hasContentIssue false
  • English
  • Français

The distribution of quadratic residues and non-residues

Published online by Cambridge University Press:  26 February 2010

D. A. Burgess
D. A. Burgess
Affiliation:
Department of Mathematics, University College, London.
Get access

Extract

If p is a prime other than 2, half of the numbers

1, 2, … p—1

are quadratic residues (mod p) and the other half are quadratic non-residues. Various questions have been proposed concerning the distribution of the quadratic residues and non-residues for large p, but as yet only very incomplete answers to these questions are known. Many of the known results are deductions from the inequality

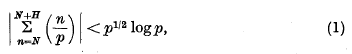
found independently by Pólya and Vinogradov, the symbol 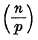being Legendre's symbol of quadratic character.

Type
Research Article
Information
Mathematika , Volume 4 , Issue 2 , December 1957 , pp. 106 - 112
Copyright
Copyright © University College London 1957

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

page 106 note * Pólya, G., “Über die Verteilung der quadratischen Reste und Nichtreste”, Göttinger Nachrichten (1918), 21–29.Google Scholar

page 106 note † Vinogradov, I. M., “Sur la distribution des résidus et des non-résidus des puissances”, Journal Physico-Math. Soc. Univ. Perm, No. 1 (1918), 94–96.Google Scholar

page 106 note ‡ Davenport, H. and Erdös, P., “The distribution of quadratic and higher residues”, Publicationes Mathematicae (Debrecen), 2 (1952), 252–265.Google Scholar

page 106 note § Vinogradov, I. M., “On a general theorem concerning the distribution of the residues and non-residues of powers”, Trans. American Math. Soc., 29 (1927), 209–217.CrossRefGoogle Scholar

page 107 note * See Landau, E., Vorlesungen über Zahlentheorie II, 178–180.Google Scholar

page 107 note † Weil, A., “Sur les courbes algébriques et les variétés qui s'en déduisent”, Actualiés Math, et Sci., No. 1041 (1945), Deuxième partie, §IV.Google Scholar

page 107 note ‡ See Hasse, H., “Theorie der relativ-zyklischen algebraischen Funktionenkörper, insbesondere bei endlichem Konstantenkörper”, Journal für Math., 172 (1935), 37–54.Google Scholar