Hostname: page-component-586b7cd67f-2brh9 Total loading time: 0 Render date: 2024-11-23T05:05:41.296Z Has data issue: false hasContentIssue false
  • English
  • Français

ASYMPTOTIC LINEAR PROGRAMMING LOWER BOUNDS FOR THE ENERGY OF MINIMIZING RIESZ AND GAUSS CONFIGURATIONS

Part of: Classical measure theory Other generalizations

Published online by Cambridge University Press:  27 September 2018

D. P. Hardin ,
T. J. Michaels  and
E. B. Saff
D. P. Hardin
Affiliation:
Center for Constructive Approximation, Department of Mathematics, Vanderbilt University, Nashville, TN 37240, U.S.A. email [email protected]
T. J. Michaels
Affiliation:
Center for Constructive Approximation, Department of Mathematics, Vanderbilt University, Nashville, TN 37240, U.S.A. email [email protected]
E. B. Saff
Affiliation:
Center for Constructive Approximation, Department of Mathematics, Vanderbilt University, Nashville, TN 37240, U.S.A. email [email protected]
Get access

Abstract

Utilizing frameworks developed by Delsarte, Yudin and Levenshtein, we deduce linear programming lower bounds (as 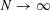$N\rightarrow \infty$) for the Riesz energy of 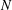$N$-point configurations on the 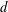$d$-dimensional unit sphere in the so-called hypersingular case; i.e., for non-integrable Riesz kernels of the form 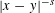$|x-y|^{-s}$ with 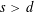$s>d$. As a consequence, we immediately get (thanks to the poppy-seed bagel theorem) lower estimates for the large 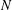$N$ limits of minimal hypersingular Riesz energy on compact 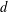$d$-rectifiable sets. Furthermore, for the Gaussian potential 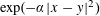$\exp (-\unicode[STIX]{x1D6FC}|x-y|^{2})$ on 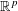$\mathbb{R}^{p}$, we obtain lower bounds for the energy of infinite configurations having a prescribed density.

MSC classification

Primary: 28A78: Hausdorff and packing measures 31C20: Discrete potential theory and numerical methods
Type
Research Article
Information
Mathematika , Volume 65 , Issue 1 , 2019 , pp. 157 - 180
Copyright
Copyright © University College London 2018 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

The research of the authors was supported, in part, by National Science Foundation grant DMS-1516400. The research of T. Michaels was completed as part of his PhD dissertation at Vanderbilt University. Research for this article was conducted while two of the authors were in residence at the Institute for Computational and Experimental Research in Mathematics in Providence, RI, during the “Point Configurations in Geometry, Physics and Computer Science” program supported by the National Science Foundation under Grant No. DMS-1439786 and by a Simons Foundation Targeted Grant.

References

Borodachov, S. V., Hardin, D. P. and Saff, E. B., Asymptotics of best-packing on rectifiable sets. Proc. Amer. Math. Soc. 135(8) 2007, 2369–2380.Google Scholar
Borodachov, S. V., Hardin, D. P. and Saff, E. B., Asymptotics for discrete weighted minimal Riesz energy problems on rectifiable sets. Trans. Amer. Math. Soc. 360(3) 2008, 1559–1580.Google Scholar
Borodachov, S., Hardin, D. P. and Saff, E. B., Discrete Energy on Rectifiable Sets, Springer (New York, NY), to appear.Google Scholar
Boumova, S., Applications of polynomials to spherical codes and designs. PhD Thesis, Eindhoven University of Technology, 2002.Google Scholar
Boyvalenkov, P., Dragnev, P., Hardin, D. P., Saff, E. B. and Stoyanova, M., Universal lower bounds for potential energy of spherical codes. Constr. Approx. 44(3) 2016, 385–415.Google Scholar
Brauchart, J. S., Hardin, D. P. and Saff, E. B., The next-order term for optimal Riesz and logarithmic energy asymptotics on the sphere. In Recent Advances in Orthogonal Polynomials, Special Functions, and their Applications (Contemporary Mathematics 578 ), American Mathematical Society (Providence, RI, 2012), 31–61.Google Scholar
Cohn, H. and de Courcy-Ireland, M., The Gaussian core model in high dimensions. Preprint, 2016, arXiv:1603.09684.Google Scholar
Cohn, H. and Kumar, A., Universally optimal distribution of points on spheres. J. Amer. Math. Soc. 10 2006, 99–148.Google Scholar
Cohn, H., Kumar, A., Miller, S., Radchecnko, D. and Viazovska, M., The sphere packing problem in dimension 24. Ann. of Math. (2) 185(3) 2017, 1017–1033.Google Scholar
Conway, J. H. and Sloane, N. J. A., Sphere Packings, Lattices and Groups, 3rd edn (Grundlehren der mathematischen Wissenschaften [Fundamental Principles of Mathematical Sciences] 290 ), Springer (New York, NY, 1999).Google Scholar
Delsarte, P., Bounds for unrestricted codes, by linear programming. Philips Res. Rep. 27 1972, 272–289.Google Scholar
Delsarte, P., Goethals, J. M. and Seidel, J. J., Spherical codes and designs. Geom. Dedicata 6(3) 1977, 363–388.Google Scholar
Erdelyi, T., Magnus, A. P. and Nevai, P., Generalized Jacobi weights, Christoffel functions, and Jacobi polynomials. SIAM J. Math. Anal. 25 1994, 602–614.Google Scholar
Hardin, D. P., Leblé, T., Saff, E. B. and Serfaty, S., Large deviation principles for hypersingular Riesz gases. Constr. Approx. 48(1) 2018, 61–100.Google Scholar
Hardin, D. P. and Saff, E. B., Minimal Riesz energy point configurations for rectifiable d-dimensional manifolds. Adv. Math. 193(1) 2005, 174–204.Google Scholar
Koelink, E., de los Ríos, A. M. and Román, P., Matrix-valued Gegenbauer-type polynomials. Constr. Approx. 46(3) 2017, 459–487.Google Scholar
Kuijlaars, A. B. J. and Saff, E. B., Asymptotics for minimal discrete energy on the sphere. Trans. Amer. Math. Soc. 350(2) 1998, 523–538.Google Scholar
Landkof, N. S., Foundations of Modern Potential Theory (Grundlehren der mathematischen Wissenschaften [Fundamental Principles of Mathematical Sciences] 180 ), Springer (New York, NY, 1972).Google Scholar
Levenshtein, V. I., Bounds for packings in n-dimensional Euclidean space. Soviet Math. Dokl. 20 1979, 417–421.Google Scholar
Levenshtein, V. I., Designs as maximum codes in polynomial metric spaces. Acta Appl. Math. 29(1–2) 1992, 1–82.Google Scholar
Levenshtein, V. I., Universal bounds for codes and designs. In Handbook of Coding Theory (eds Pless, V. and Huffman, W. C.), Ch. 6, Elsevier (Amsterdam, 1998), 499–648.Google Scholar
Martinez-Finkelshtein, A., Maymeskul, V., Rakhmanov, E. A. and Saff, E. B., Asymptotics for minimal discrete Riesz energy on curves in ℝ d . Canad. J. Math. 56(3) 2004, 529–552.Google Scholar
Michaels, T. J., Node generation on surfaces and bounds on minimal Riesz energy. PhD Thesis, Vanderbilt University, Nashville, TN, 2017.Google Scholar
Pacharoni, I. and Zurrián, I., Matrix Gegenbauer polynomials: the 2 × 2 fundamental cases. Constr. Approx. 43(2) 2016, 253–271.Google Scholar
Ramanujan, S., On certain arithmetical functions [Trans. Cambridge Philos. Soc. 22(9) (1916) 159–184]. In Collected Papers of Srinivasa Ramanujan, AMS Chelsea (Providence, RI, 2000), 136–162.Google Scholar
Szegő, G., Orthogonal Polynomials, 4th edn (Colloquium Publications, XXIII ), American Mathematical Society (Providence, RI, 1975).Google Scholar
Terras, A., Harmonic analysis on symmetric spaces and applications. In Harmonic Analysis on Symmetric Spaces and Applications, Vol. 1, Springer (New York, NY, 1988).Google Scholar
Viazovska, M., The sphere packing problem in dimension 8. Ann. of Math. (2) 185(3) 2017, 991–1015.Google Scholar
Watson, G. N., A Treatise on the Theory of Bessel Functions (Cambridge Mathematical Library), reprint of 2nd (1944) edn, Cambridge University Press (Cambridge, 1995).Google Scholar
Widder, D. V., The Laplace Transform (Princeton Mathematical Series 6 ), Princeton University Press (Princeton, NJ, 1941).Google Scholar
Yudin, V. A., Minimum potential energy of a point system of charges. Diskret. Mat. 4(2) 1992, 115–121.Google Scholar