Hostname: page-component-cd9895bd7-p9bg8 Total loading time: 0 Render date: 2024-12-27T22:22:41.608Z Has data issue: false hasContentIssue false
  • English
  • Français

ANALYSIS IN THE MULTI-DIMENSIONAL BALL

Part of: Harmonic analysis in several variables Other generalizations Nontrigonometric harmonic analysis

Published online by Cambridge University Press:  31 October 2018

Peter Sjögren  and
Tomasz Z. Szarek
Peter Sjögren
Affiliation:
Department of Mathematical Sciences, Chalmers University of Technology and University of Gothenburg, SE-412 96 Göteborg, Sweden email [email protected]
Tomasz Z. Szarek
Affiliation:
Institute of Mathematics, Polish Academy of Sciences, Śniadeckich 8, 00–656 Warszawa, Poland Department of Mathematics, Informatics and Mechanics, University of Warsaw, Banacha 2, 02–097 Warszawa, Poland email [email protected]
Get access

Abstract

We study the heat semigroup maximal operator associated with a well-known orthonormal system in the 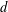$d$-dimensional ball. The corresponding heat kernel is shown to satisfy Gaussian bounds. As a consequence, we can prove weighted 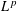$L^{p}$ estimates, as well as some weighted inequalities in mixed norm spaces, for this maximal operator.

MSC classification

Primary: 42B25: Maximal functions, Littlewood-Paley theory
Secondary: 42C05: Orthogonal functions and polynomials, general theory 31C25: Dirichlet spaces
Type
Research Article
Information
Mathematika , Volume 65 , Issue 2 , 2019 , pp. 190 - 212
Copyright
Copyright © University College London 2018 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

The second author was partially supported by the National Science Centre of Poland, project no. 2015/19/D/ST1/01178, and by the Foundation for Polish Science START Scholarship.

References

Ciaurri, Ó., The Poisson operator for orthogonal polynomials in the multidimensional ball. J. Fourier Anal. Appl. 19 2013, 1020–1028.Google Scholar
Coulhon, T., Kerkyacharian, G. and Petrushev, P., Heat kernel generated frames in the setting of Dirichlet spaces. J. Fourier Anal. Appl. 18 2012, 995–1066.Google Scholar
Dai, F. and Xu, Y., Approximation Theory and Harmonic Analysis on Spheres and Balls (Springer Monographs in Mathematics), Springer (New York, NY, 2013).Google Scholar
Dunkl, C. F. and Xu, Y., Orthogonal Polynomials of Several Variables, Cambridge University Press (Cambridge, 2001).Google Scholar
Duoandikoetxea, J., Extrapolation of weights revisited: new proofs and sharp bounds. J. Funct. Anal. 260 2011, 1886–1901.Google Scholar
Fukushima, M., Oshima, Y. and Takeda, M., Dirichlet Forms and Symmetric Markov Processes (De Gruyter Studies in Mathematics 19 ), De Gruyter (Berlin, 2011).Google Scholar
Gyrya, P. and Saloff-Coste, L., Neumann and Dirichlet Heat Kernels in Inner Uniform Domains (Astérisque 336 ), Société Mathématique de France (2011).Google Scholar
Hebisch, W. and Saloff-Coste, L., On the relation between elliptic and parabolic Harnack inequalities. Ann. Inst. Fourier (Grenoble) 51 2001, 1437–1481.Google Scholar
Kerkyacharian, G., Petrushev, P. and Xu, Y., Gaussian bounds for the weighted heat kernels on the interval, ball and simplex. Preprint, 2018, arXiv:1801.07325.Google Scholar
Kerkyacharian, G., Petrushev, P. and Xu, Y., Gaussian bounds for the heat kernels on the ball and simplex: Classical approach. Preprint, 2018, arXiv:1801.07326.Google Scholar
Saloff-Coste, L., Aspects of Sobolev-type Inequalities (London Mathematical Society Lecture Note Series 289 ), Cambridge University Press (Cambridge, 2002).Google Scholar
Szegö, G., Orthogonal Polynomials, 4th edn (Colloquium Publications 23 ), American Mathematical Society (Providence, RI, 1975).Google Scholar