Hostname: page-component-cd9895bd7-jn8rn Total loading time: 0 Render date: 2024-12-24T12:59:50.884Z Has data issue: false hasContentIssue false
  • English
  • Français

ON SELMER GROUPS OF QUADRATIC TWISTS OF ELLIPTIC CURVES WITH A TWO-TORSION OVER 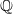$\mathbb {Q}$

Part of: Multiplicative number theory Curves Exponential sums and character sums Arithmetic algebraic geometry

Published online by Cambridge University Press:  15 January 2013

Maosheng Xiong
Maosheng Xiong*
Affiliation:
Department of Mathematics, Hong Kong University of Science and Technology, Clear Water Bay, Kowloon, Hong Kong (email: [email protected])
Get access

Abstract

We study the distribution of the size of Selmer groups arising from a 2-isogeny and its dual 2-isogeny for quadratic twists of elliptic curves with a non-trivial 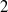$2$-torsion point over 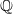$\mathbb {Q}$. This complements the work [Xiong and Zaharescu, Distribution of Selmer groups of quadratic twists of a family of elliptic curves. Adv. Math.219 (2008), 523–553] which studied the same subject for elliptic curves with full 2-torsions over 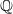$\mathbb {Q}$ and generalizes [Feng and Xiong, On Selmer groups and Tate–Shafarevich groups for elliptic curves 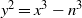$y^2=x^3-n^3$. Mathematika 58 (2012), 236–274.] for the special elliptic curves 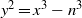$y^2=x^3-n^3$. It is shown that the 2-ranks of these groups all follow the same distribution and in particular, the mean value is 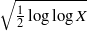$\sqrt {\frac {1}{2}\log \log X}$ for square-free positive integers 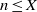$n \le X$ as 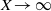$X \to \infty $.

MSC classification

Secondary: 11G05: Elliptic curves over global fields 11L40: Estimates on character sums 11N45: Asymptotic results on counting functions for algebraic and topological structures 14H52: Elliptic curves
Type
Research Article
Information
Mathematika , Volume 59 , Issue 2 , July 2013 , pp. 303 - 319
Copyright
Copyright © 2013 University College London 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

[1]Atake, D., On elliptic curves with large Tate–Shafarevich groups. J. Number Theory 87 (2001), 282–300.CrossRefGoogle Scholar
[2]Chang, S., Note on the rank of quadratic twists of Mordell equations. J. Number Theory 118(1) (2006), 53–61.CrossRefGoogle Scholar
[3]Feng, K. and Xiong, M., On Selmer groups and Tate–Shafarevich groups for elliptic curves$y^2=x^3-n^3$. Mathematika 58 (2012), 236–274.CrossRefGoogle Scholar
[4]Goldfeld, D., Conjectures on elliptic curves over quadratic fields. In Number Theory, Carbondale 1979 (Proc. Southern Illinois Conf., Southern Illinois Univ., Carbondale, Ill., 1979) (Lecture Notes in Mathematics 751) (ed. Nathanson, M. B.), Springer (Berlin, 1979), 108–118.Google Scholar
[5]Granville, A. and Soundararajan, K., Sieving and the Erdős–Kac theorem. In Equidistribution in Number Theory, an Introduction (NATO Science Series II: Mathematics, Physics and Chemistry 237), Springer (Dordrecht, 2007), 15–27.Google Scholar
[6]Harris, J. M., Hirst, J. L. and Mossignhoff, M. J., Combinatorics and Graph Theory, Springer (Berlin, 2000).CrossRefGoogle Scholar
[7]Heath-Brown, D. R., The size of Selmer groups for the congruent number problem, I. Invent. Math. 111 (1993), 171–195.CrossRefGoogle Scholar
[8]Heath-Brown, D. R., The size of Selmer groups for the congruent number problem, II. Invent. Math. 118 (1994), 331–370.CrossRefGoogle Scholar
[9]Silverman, J. H., The Arithmetic of Elliptic Curves (Graduate Texts in Mathematics 106), Springer (Berlin, 1986).CrossRefGoogle Scholar
[10]Swinnerton-Dyer, P., The effect of twisting on the 2-Selmer group. Math. Proc. Cambridge Philos. Soc. 145(3) (2008), 513–526.CrossRefGoogle Scholar
[11]Xiong, M. and Zaharescu, A., Distribution of Selmer groups of quadratic twists of a family of elliptic curves. Adv. Math. 219 (2008), 523–553.CrossRefGoogle Scholar
[12]Yu, G., Rank 0 quadratic twists of a family of elliptic curves. Compositio Math. 135(3) (2003), 331–356.CrossRefGoogle Scholar
[13]Yu, G., On the quadratic twists of a family of elliptic curves. Mathematika 52(1–2) (2005), 139–154.CrossRefGoogle Scholar