Hostname: page-component-586b7cd67f-vdxz6 Total loading time: 0 Render date: 2024-11-27T01:29:28.107Z Has data issue: false hasContentIssue false
  • English
  • Français

On inductive limits of measure spaces and projective limits of Lp-spaces

Published online by Cambridge University Press:  26 February 2010

N. D. Macheras
N. D. Macheras
Affiliation:
Department of Statistics, Piraeus Graduate School of Industrial Studies, 40, Karaoli and Dimitriou Stret, 185 32 Piraeus, Greece.
Get access

Extract

The existence of inductive limits in the category of (topological) measure spaces is proved. Next, permanence properties of inductive limits are investigated. If (X, 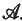, ) is the inductive limit of the measure spaces (X, 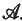, ), we prove, for 1 p 221E;, that LP(X, 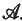, ) is embeddible into the projectilimit of Lp(X, 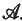, ) in the category Ban, for p < , respectively in the category C* in the case p = +. As an application, we exten existence theorems of strong liftings to inductive limits.

Type
Research Article
Information
Mathematika , Volume 36 , Issue 1 , June 1989 , pp. 116 - 130
Copyright
Copyright University College London 1989

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1.Babiker, A. G. A. G.. Some measure theoretic properties on completely regular spaces. Atti. Acad. Naz. Lincei Rend. Cl. Sci. Fis. Mat. Natur., 59 (1975), 362365, 677681.Google Scholar
2.Babiker, A. G. A. G. and Strauss, W. Almost strong liftings and T-additivity. Measure Theory. Proc. Oberwolfach, 1979, Ed. Klzow, D.. Lecture Notes in Mathematics, 794 (Springer, 1980).Google Scholar
3.Babiker, A. G. A. G. and Graf, S.. Homomorphism compact spaces. Can. J. Math. 35 (1983), 558576.Google Scholar
4.Bellow, A.. Lifting compact spaces. Measure Theory Proc. Oberwolfach, 1979. Ed. Klzow, D.. Lecture Notes in Mathematics, 794 (Springer, 1980).Google Scholar
5.Bourbaki, N.. Thorie des Ensembles (Hermann, Paris, 1970).Google Scholar
6.Dugundji, J.. Topology (Allyn and Bacon Inc., Boston, 1970).Google Scholar
7.Fremlin, D. H.. Topological Riesz Spaces and Measure Theory (Cambridge University Press, 1974).Google Scholar
8.Gardner, R. J. and Pfefler, W. F.. Conditions that imply a space is Radon. Measure Theory, Proc. Oberwolfach, 1983. Ed. Klzow, D. and Maharam, D.. Lecture Notes in Math., 1089(Springer, 1984), 1122.Google Scholar
9.Graf, S.. On the existence of strong liftings in second countable topological spaces. PacificJ. Math., 58 (1975), 419426.Google Scholar
10.Halmos, P. R.. Measure Theory (Van Nostrand Reinhold, New York, 1950).Google Scholar
11.A., and Ionescu Tulcea, C.. Topics in the Theory of Liftings (Springer, 1969).Google Scholar
12.Macheras., N. D. Permanenzprobleme fr induktive Limiten. Dissertation (UniversitatErlangen-Nurnberg, 1984).Google Scholar
13.Michael, E.. Locally multiplicatively-convex topological algebras. Mem. Amer. Math. Soc., 11 (1952), 179.Google Scholar
14.Sakai, S.. C*-Algebras and W*-Algebras (Springer, 1971).Google Scholar
15.Schwartz, L.. Radon Measures on Arbitrary "Topological Spaces and Cylindrical Measures (Oxford Univ. Press, London, 1973).Google Scholar
16.Semadeni, Z.. Banach Spaces of Continuous Functions, Vol. I (Warszawa, 1971).Google Scholar
17.Sion, M.. A Theory of Semigroup Valued Measures. Lecture Notes in Math., 355 (Springer, 1973).Google Scholar
18.Steen, L. A. and Seebach, J. A.. Counterexamples in Topology (Springer, 1978).Google Scholar
19.Vasilach, S.. Direct limits of measure spaces. J. Multivariate Analysis, 1 (1971), 394411.Google Scholar
20.Vasilach, S.. A calculus of direct limits of probability spaces. J. Multivariate Analysis, 3 (1973), 116.CrossRefGoogle Scholar
21.Vasilach, S.. Integration of direct limits of real random variables. J. Multivariate Analysis, 3 (1973), 1725.Google Scholar
22.Vasilach, S.. Some remarks on the direct limits of measure spaces. J. Multivariate Analysis, 4 (1974), 222233.Google Scholar
23Wheeler, R. F.. A survey of Baire measures and strict topologies. Exposition. Math., 1 (1983), 97190.Google Scholar