Hostname: page-component-cd9895bd7-p9bg8 Total loading time: 0 Render date: 2024-12-25T14:02:56.671Z Has data issue: false hasContentIssue false
  • English
  • Français

LONELY RUNNERS IN FUNCTION FIELDS

Part of: Diophantine approximation, transcendental number theory Extremal combinatorics Probabilistic theory: distribution modulo $1$; metric theory of algorithms Designs and configurations

Published online by Cambridge University Press:  12 April 2019

Sam Chow  and
Luka Rimanić
Sam Chow
Affiliation:
Mathematical Institute, University of Oxford, Woodstock Road, Oxford OX2 6GG, U.K. email [email protected]
Luka Rimanić
Affiliation:
School of Mathematics, University of Bristol, University Walk, Bristol BS8 1TW, U.K. email [email protected]
Get access

Abstract

The lonely runner conjecture, now over fifty years old, concerns the following problem. On a unit-length circular track, consider 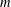$m$ runners starting at the same time and place, each runner having a different constant speed. The conjecture asserts that each runner is lonely at some point in time, meaning at a distance at least 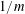$1/m$ from the others. We formulate a function field analogue, and give a positive answer in some cases in the new setting.

MSC classification

Primary: 11J71: Distribution modulo one
Secondary: 11K41: Continuous, $p$-adic and abstract analogues 05D05: Extremal set theory 05B20: Matrices (incidence, Hadamard, etc.)
Type
Research Article
Information
Mathematika , Volume 65 , Issue 3 , 2019 , pp. 677 - 701
Copyright
Copyright © University College London 2019 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Alon, N., The chromatic number of random Cayley graphs. European J. Combin. 34 2013, 1232–1243.Google Scholar
Alon, N. and Spencer, J., The Probabilistic Method, 3rd edn., John Wiley & Sons (Hoboken, NJ, 2008).Google Scholar
Barajas, J. and Serra, O., The lonely runner with seven runners. Electron. J. Combin. 15 2008, R48.Google Scholar
Betke, U. and Wills, J. M., Untere Schranken für zwei diophantische Approximations-Funktionen. Monatsh. Math. 76 1972, 214–217.Google Scholar
Biennia, W., Goddyn, L., Gvozdjak, P., Sebő, A. and Tarsi, M., Flows, view obstructions and the lonely runner. J. Combin. Theory Ser. B 72 1998, 1–9.Google Scholar
Bohman, T., Holzman, R. and Kleitman, D., Six lonely runners. Electron. J. Combin. 8(2) 2001, R3.Google Scholar
Chen, Y. G., View-obstruction problems in n-dimensional Euclidean space and a generalization of them. Acta Math. Sinica 37 1994, 551–562.Google Scholar
Chen, Y. G. and Cusick, T. W., The view-obstruction problems for n-dimensional cubes. J. Number Theory 74 1999, 126–133.Google Scholar
Cusick, T. W., View-obstruction problems. Aequationes Math. 9 1973, 165–170.Google Scholar
Cusick, T. W., View-obstruction problems in n-dimensional geometry. J. Combin. Theory Ser. A 16 1974, 1–11.Google Scholar
Cusick, T. W., View-obstruction problems II. Proc. Amer. Math. Soc. 84 1982, 25–28.Google Scholar
Cusick, T. W. and Pomerance, C., View-obstruction problems III. J. Number Theory 19 1984, 131–139.Google Scholar
Czerwiński, S., Random runners are very lonely. J. Combin. Theory Ser. A 119 2012, 1194–1199.Google Scholar
Czerwiński, S. and Grytczuk, J., Invisible runners in finite fields. Inform. Process. Lett. 108 2008, 64–67.Google Scholar
Davis, P. J., Circulant Matrices, 2nd edn., AMS Chelsea Publishing (New York, 1994).Google Scholar
Dubickas, A., The lonely runner problem for many runners. Glas. Mat. Ser. III 46(66) 2011, 25–30.Google Scholar
Ellenberg, J. S., Venkatesh, A. and Westerland, C., Homological stability for Hurwitz spaces and the Cohen–Lenstra conjecture over function fields. Ann. of Math. (2) 183 2016, 729–786.Google Scholar
Entin, A., On the Bateman–Horn conjecture for polynomials over large finite fields. Compos. Math. 152 2016, 2525–2544.Google Scholar
Etzion, T. and Raviv, N., Equidistant codes in the Grassmannian. Discrete Appl. Math. 186 2015, 87–97.Google Scholar
Ganguly, A. and Ghosh, A., Dirichlet’s theorem in function fields. Canad. J. Math. 69 2017, 532–547.Google Scholar
Hegedüs, G., An improved upper bound for the size of a sunflower-free family. Acta Math. Hungar. 155 2018, 431–438.Google Scholar
Jukna, S., Extremal Combinatorics. With Applications in Computer Science (Texts in Theoretical Computer Science, an EATCS series), 2nd edn., Springer (Heidelberg, 2011).Google Scholar
Katz, N. and Sarnak, P., Random Matrices, Frobenius Eigenvalues and Monodromy (AMS Colloquium Publications 45 ), AMS (Providence, RI, 1999).Google Scholar
Katz, N. and Sarnak, P., Zeros of zeta functions and symmetries. Bull. Amer. Math. Soc. 36 1999, 1–26.Google Scholar
Liu, Y.-R. and Wooley, T. D., Waring’s problem in function fields. J. Reine Angew. Math. 638 2010, 1–67.Google Scholar
Naslund, E. and Sawin, W. F., Upper bounds for sunflower-free sets. Forum Math. Sigma 5 2017, e15.Google Scholar
Perarnau, G. and Serra, O., Correlation among runners and some results on the lonely runner conjecture. Electron. J. Comb. 23 2016, P1.50.Google Scholar
Rauhut, H., Romberg, J. and Tropp, J. A., Restricted isometries for partial random circulant matrices. Appl. Comput. Harmon. Anal. 32 2012, 242–254.Google Scholar
Renault, J., View-obstruction: a shorter proof for 6 lonely runners. Discrete Math. 287 2004, 93–101.Google Scholar
Tao, T., Some remarks on the lonely runner conjecture. Contrib. Discrete Math. 13(2) 2018, 1–31.Google Scholar
van der Geer, G., Moonen, B. and Schoof, R. (eds), Number fields and function fields—two parallel worlds (Progress in Mathematics 239 ), Birkhäuser (Boston, 2005).Google Scholar
Vaughan, R. C., The Hardy–Littlewood Method (Cambridge Tracts in Mathematics 125 ), 2nd edn., Cambridge University Press (Cambridge, 1997).Google Scholar
Weber, H. and Dedekind, R., Theorie der algebraischen Functionen einer Veränderlichen. J. Reine Angew. Math. 92 1882, 181–290.Google Scholar
Weil, A., On the Riemann hypothesis in function-fields. Proc. Nat. Acad. Sci. USA 27 1941, 345–347.Google Scholar
Wills, J. M., Zwei Säzte über inhomogene diophantische Approximation von Irrationalzahlen. Monatsh. Math. 71 1967, 263–269.Google Scholar
Yin, W., Morgan, S., Yang, J. and Zhang, Y., Practical compressive sensing with Toeplitz and circulant matrices. In Visual Communications and Image Processing 2010 (Proc. SPIE 7744 ), SPIE (Bellingham, WA, 2010).Google Scholar