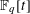 $\mathbb{F}_{q}[t]$
$\mathbb{F}_{q}[t]$Published online by Cambridge University Press: 05 March 2019
We examine correlations of the Möbius function over 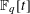 $\mathbb{F}_{q}[t]$ with linear or quadratic phases, that is, averages of the form 1
$\mathbb{F}_{q}[t]$ with linear or quadratic phases, that is, averages of the form 1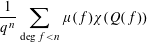 $$\begin{eqnarray}\frac{1}{q^{n}}\mathop{\sum }_{\deg f<n}\unicode[STIX]{x1D707}(f)\unicode[STIX]{x1D712}(Q(f))\end{eqnarray}$$
$$\begin{eqnarray}\frac{1}{q^{n}}\mathop{\sum }_{\deg f<n}\unicode[STIX]{x1D707}(f)\unicode[STIX]{x1D712}(Q(f))\end{eqnarray}$$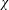 $\unicode[STIX]{x1D712}$ over
$\unicode[STIX]{x1D712}$ over 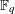 $\mathbb{F}_{q}$ and a polynomial
$\mathbb{F}_{q}$ and a polynomial 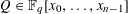 $Q\in \mathbb{F}_{q}[x_{0},\ldots ,x_{n-1}]$ of degree at most 2 in the coefficients
$Q\in \mathbb{F}_{q}[x_{0},\ldots ,x_{n-1}]$ of degree at most 2 in the coefficients 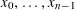 $x_{0},\ldots ,x_{n-1}$ of
$x_{0},\ldots ,x_{n-1}$ of 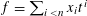 $f=\sum _{i<n}x_{i}t^{i}$. As in the integers, it is reasonable to expect that, due to the random-like behaviour of
$f=\sum _{i<n}x_{i}t^{i}$. As in the integers, it is reasonable to expect that, due to the random-like behaviour of 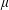 $\unicode[STIX]{x1D707}$, such sums should exhibit considerable cancellation. In this paper we show that the correlation (1) is bounded by
$\unicode[STIX]{x1D707}$, such sums should exhibit considerable cancellation. In this paper we show that the correlation (1) is bounded by 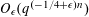 $O_{\unicode[STIX]{x1D716}}(q^{(-1/4+\unicode[STIX]{x1D716})n})$ for any
$O_{\unicode[STIX]{x1D716}}(q^{(-1/4+\unicode[STIX]{x1D716})n})$ for any 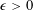 $\unicode[STIX]{x1D716}>0$ if
$\unicode[STIX]{x1D716}>0$ if 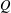 $Q$ is linear and
$Q$ is linear and 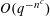 $O(q^{-n^{c}})$ for some absolute constant
$O(q^{-n^{c}})$ for some absolute constant 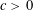 $c>0$ if
$c>0$ if 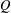 $Q$ is quadratic. The latter bound may be reduced to
$Q$ is quadratic. The latter bound may be reduced to 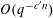 $O(q^{-c^{\prime }n})$ for some
$O(q^{-c^{\prime }n})$ for some 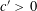 $c^{\prime }>0$ when
$c^{\prime }>0$ when 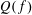 $Q(f)$ is a linear form in the coefficients of
$Q(f)$ is a linear form in the coefficients of 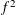 $f^{2}$, that is, a Hankel quadratic form, whereas, for general quadratic forms, it relies on a bilinear version of the additive-combinatorial Bogolyubov theorem.
$f^{2}$, that is, a Hankel quadratic form, whereas, for general quadratic forms, it relies on a bilinear version of the additive-combinatorial Bogolyubov theorem.