Hostname: page-component-78c5997874-lj6df Total loading time: 0 Render date: 2024-11-05T13:24:49.961Z Has data issue: false hasContentIssue false
  • English
  • Français

Decomposition of flat manifolds

Part of: Global differential geometry

Published online by Cambridge University Press:  26 February 2010

Andrzej Szczepański
Andrzej Szczepański
Affiliation:
Institute of Mathematics, University of Gdańsk, ul. Wita Stwosza 57, 80-952 Gdańsk, Poland. E-mail: [email protected]
Get access

Extract

Let M be a compact flat Riemannian manifold of dimension n, and Γ its fundamental group. Then we have the following exact sequence (see [1])

where Zn is a maximal abelian subgroup of Γ and G is a finite group isomorphic to the holonomy group of M. We shall call Γ a Bieberbach group. Let T be a flat torus, and let Ggr act via isometries on T; then ┌ acts isometrically on 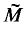× T where 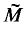is the universal covering of M and yields a flat Riemannian structure on ( 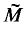× T)/Γ. A flat-toral extension (see [9, p. 371]) of the Riemannian manifold M is any Riemannian manifold isometric to ( 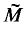× T)/Γ where T is a flat torus on which Γ acts via isometries. It is convenient to adopt the convention that a single point is a 0-dimensional flat torus. If this is done, M is itself among the flat toral extensions of M. Roughly speaking, this is a way of putting together a compact flat manifold and a flat torus to make a new flat manifold the dimension of which is the sum of the dimensions of its constituents. It is, more precisely, a fibre bundle over the flat manifold with a flat torus as fibre.

MSC classification

Secondary: 53C10: $G$-structures
Type
Research Article
Information
Mathematika , Volume 44 , Issue 1 , June 1997 , pp. 113 - 119
Copyright
Copyright © University College London 1997

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1.Charlap, L. S.. Bieherbach Groups and Flat Manifolds (Springer-Verlag, New York, 1986).CrossRefGoogle Scholar
2.Cliff, G. and Weiss, A.. Torsion free space groups and permutation lattices for finite groups. Contemporary Mathem., 93 (1989), 123–132.CrossRefGoogle Scholar
3.Curtis, C. W. and Reiner, I.. Methods of Representation Theory (John Wiley, 1987).Google Scholar
4.Hamrick, G. C. and Royster, D. C.. Flat Riemannian manifolds are boundaries. Invent. Math., 66 (1982), 405–413.CrossRefGoogle Scholar
5.Hiller, H. and Sah, C. H.. Holonomy of flat manifolds with b 1=0, I. Quarterly J. Math. Oxford, 37 (1986), 177–187.CrossRefGoogle Scholar
6.Kargapolov, M. I. and Merzljakov, Ju. I.. Fundamentals of the Theory of Groups (Springer-Verlag, 1979).CrossRefGoogle Scholar
7.Plesken, W.. Some applications of representation theory. In Representation theory of finite groups and finite dimensional algebras. Progress in Mathematics, 95 (Birkhauser, Basel, 1991).Google Scholar
8.Symonds, P.. Localization in the classification of flat manifolds. Pac. J. of Math., 127 (1987), 389–399.CrossRefGoogle Scholar
9.Vasquez, A. T.. Flat Riemannian manifolds. J. Diff. Geom., 4 (1970), 367–382.Google Scholar
10.Yau, S. T.. Compact flat Riemannian manifolds, J. Diff. Geom., 6 (1972), 395–402.Google Scholar