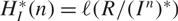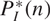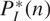Research Article
Tight closure of powers of ideals and tight hilbert polynomials
- Part of:
-
- Published online by Cambridge University Press:
- 12 July 2019, pp. 335-355
-
- Article
- Export citation
Semantics of higher inductive types
- Part of:
-
- Published online by Cambridge University Press:
- 17 June 2019, pp. 159-208
-
- Article
- Export citation
Open manifolds with non-homeomorphic positively curved souls
- Part of:
-
- Published online by Cambridge University Press:
- 11 July 2019, pp. 357-376
-
- Article
- Export citation
Front Cover (OFC, IFC) and matter
PSP volume 169 issue 3 Cover and Front matter
-
- Published online by Cambridge University Press:
- 29 October 2020, pp. f1-f2
-
- Article
-
- You have access
- Export citation
Research Article
Hilbert’s 16th problem on a period annulus and Nash space of arcs
- Part of:
-
- Published online by Cambridge University Press:
- 12 July 2019, pp. 377-409
-
- Article
- Export citation
Back Cover (OBC, IBC) and matter
PSP volume 169 issue 3 Cover and Back matter
-
- Published online by Cambridge University Press:
- 29 October 2020, pp. b1-b5
-
- Article
-
- You have access
- Export citation
Research Article
Triforce and corners
- Part of:
-
- Published online by Cambridge University Press:
- 12 July 2019, pp. 209-223
-
- Article
- Export citation
On the residual and profinite closures of commensurated subgroups
- Part of:
-
- Published online by Cambridge University Press:
- 30 July 2019, pp. 411-432
-
- Article
- Export citation
Front Cover (OFC, IFC) and matter
PSP volume 169 issue 1 Cover and Front matter
-
- Published online by Cambridge University Press:
- 07 July 2020, pp. f1-f2
-
- Article
-
- You have access
- Export citation
PSP volume 169 issue 2 Cover and Front matter
-
- Published online by Cambridge University Press:
- 18 August 2020, pp. f1-f2
-
- Article
-
- You have access
- Export citation
Back Cover (OBC, IBC) and matter
PSP volume 169 issue 1 Cover and Back matter
-
- Published online by Cambridge University Press:
- 07 July 2020, pp. b1-b2
-
- Article
-
- You have access
- Export citation
PSP volume 169 issue 2 Cover and Back matter
-
- Published online by Cambridge University Press:
- 18 August 2020, pp. b1-b2
-
- Article
-
- You have access
- Export citation

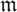 ) be an analytically unramified local ring of positive prime characteristic
) be an analytically unramified local ring of positive prime characteristic