It is trivial that a group all of whose elements except the identity have order two is Abelian; and F. Levi and B. L. van der Waerden(1) have shown that a group all of whose elements except the identity have order three has class less than or equal to three. On the other hand, R. Baer(3) has shown that if the fact that all the elements of a group have orders dividing n implies a limitation on the class of the group, then n is a prime. The object of the present note is to extend this result by showing that if M is a fixed integer there are at most a finite number of prime powers n other than primes, such that the fact that all the elements of a group have orders dividing n implies a limitation on the class of its Mth derived group.

Blichfeldt (2) gave a method of proving the existence of lattice points in certain regions. His method depends on the following lemma (which he stated in a somewhat different form):

Lemma 1. Let K′ be a closed region of volume V. Let K be another region so related to K′ that the difference of any two points in K′ is a point in K. Let Λ be any lattice whose determinant is positive and does not exceed V.

1. In this note we shall prove the

Theorem 1. Letbe a linear space of (real or complex) functions f(s) defined in the interval 0 ≤ s ≤ 1 subject to the following two conditions:

(i) every function of the infinite sequence 1, s, s2, …, sn, … is an element of;

(ii) two elements, f(s) and g(s), ofare to be considered as distinct if, and only if, they differ on a set of positive measure in the interval 0 ≤ s ≤ 1.

1. The problem in question is to find a necessary and sufficient condition which numbers co, …, cm must satisfy in order that there shall be a non-decreasing function σ(t) such that

where (a, b) is an unbounded interval. (When (a, b) is a bounded interval, the problem has been solved. See Achyèser and Krein, Communications de la Société Mathématique de Kharkoff, Série 4, 12 (1935), 13–35, Satz C.)

1. The particular set of symmetric polynomials known as S-functions has recently been shown to be of importance in a variety of algebraic problems. Many of the applications of these functions depend upon the properties of the operation which Littlewood terms ‘new multiplication’, by which, from two given S-functions {μ}, {ν} of respective degrees m and n, is constructed a symmetric function {μ} ⊗ {ν} of degree mn. Littlewood has devoted a considerable part of his paper (2) to explaining various methods by which this function can be expressed in terms of S-functions of degree mn. None of these methods is really simple (in the sense that the rule for expressing the ordinary product {μ} {ν} in terms of S-functions of degree m + n is simple); and, indeed, it would be unreasonable to expect any simple rule of general validity for writing the resulting expression down since, for instance, a knowledge of the explicit expression for {μ} ⊗ {n} would yield immediately a knowledge of all the linearly independent concomitants, of degree n, of an algebraic form of type {μ} in an arbitrary number of variables. Nevertheless, the evaluation of {μ} ⊗ {ν} in particular cases is often necessary. Of the methods suggested by Littlewood for performing this evaluation the one which seems to be normally the simplest (his ‘third method’) involves a process which is not shown to be free from ambiguity, and which can actually be shown by examples to give, in certain cases, alternative solutions, the choice between which must be made by other considerations. It is therefore perhaps worth while putting on record a quite different method of procedure, which, apart from any intrinsic interest which it may possess, seems to be quite practicable for most of the actual evaluations performed by Littlewood.

We shall first give some definitions concerning parametric surfaces. Denote by H a closed circle (disk) and by M a variable point on it. Let P = Ф(M) be a continuous function on H whose value P is a point in three-dimensional space. The symbols Ф(E), Ф−1(P), where E is a set of points on H and P a point in the three-dimensional space, will have their usual meaning. Ф−1(P) is a closed set. Any saturated continuum in Ф−1(P) or any point of Ф−1(P) that does not belong to such continua is called a Ф-element of H. Thus to any continuous function Ф(M) corresponds a representation of H in the form of the sum σQ of Ф-elements. The set of the pairs (P, Q), where Q runs through all Ф-elements of H and, for any Q, P = Ф(Q), is called a parametric surface, and any pair (P, Q) is called a point of the parametric surface. We shall often speak of a point Ф(M) of the parametric surface, by which we shall mean either the point (P, Q), where P = Ф(M) and Q is the Ф-element containing M, or the point P = Ф(M) of the three-dimensional space. The exact meaning will always be clear from the context. If there are exactly k points of the parametric surface whose first member is P0 we say that P0 is a point of multiplicity k. If k = 1, P0 is a simple point.

1. The problem of automatic synchronization of triode oscillators was studied by Appleton† and van der Pol‡; it gives rise to the differential equation

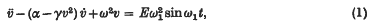
where α, γ, ω, E, ω1 are positive constants such that α/ω, γ/ω, (ω − ω1)/ω are small and dots denote differentiations with respect to t. When these conditions are satisfied, it is easy to see that

is an approximate solution over a limited time for any b1, b2 chosen to fit initial conditions on v and ṿ provided that v and ṿ are not too large. If it is assumed that b1 and b2 vary slowly compared with ω1t, so that 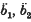can be neglected, and ḃ1, ḃ2 are comparatively small, the equations

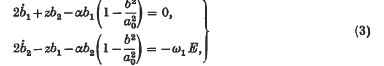
where

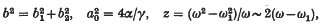
are obtained. These are sufficiently accurate for the discussion of most of the physical phenomena, and have been used in this form (or in the polar-coordinate form obtained by putting b1 = b cos ø, b2 = b sin ø) by various authors §. Solutions of (1) with period 2π/ω1 are obtained approximately by putting ḃ1 = ḃ2 = 0 in (3). The steady-state solutions of (1) other than those with period 2π/ω1 correspond to periodic solutions of (3). All other solutions converge to one or other of these types of solution.

Let x = ℘′(u) and y = ½℘(u), where the Weierstrass ℘-function has invariants g2 = 4A, g3 = 4B and differentiation with respect to the parameter u is denoted by a dash, so that

The name ‘cardinal function’ was given to

by E. T. Whittaker (1), who considered it as a ‘smooth’ approximation to a function f(x), having the same values as f(x) at the points a + rw (r = 0, ± 1, ± 2, …). It has since been extensively studied (2), mainly from the point of view of interpolation theory. Hardy (3), however, observed that the functions νr(t) defined by

form a normal orthogonal set on the interval (−∞, ∞), for r = 0, ± 1, ± 2, …. This fact suggests a discussion of the cardinal series from the point of view of mean-square approximation.

1·1. There is a familiar method of summation of series usually called the method (R, 1), or sometimes Lebesgue's method. If sn = u0 + u1 + … + un and, as it will be convenient to suppose throughout, u0 = 0, then

when h → + 0§ the convergence of the series for small positive h is presupposed. The method is not 'regular'; there are convergent series not summable (R, 1).

The inequality which is proved here was established under different conditions in a paper entitled ‘Periodic points on an algebraic variety', which is to appear in the Annals of Mathematics. It is hoped that the new formulation will be more useful for applications. The present investigations use the rather sophisticated techniques of the ‘Theory of distributions’ which was developed by Weil (1). As the content of this theory may be unfamiliar to the reader, Weil's results are described at some length, though of course, his proofs are not given. The one result which we need and which is not given explicitly by Weil, is proved in detail.

In 1914 Carathéodory defined m–dimensional measure in n–dimensional space. He considered one-dimensional measure as a generalization of length and he proved that the length of a rectifiable curve coincides with its one-dimensional measure.

A sequence of papers by P. Hall ((1)–(4)) on some fundamental properties of soluble groups was followed in 1940 by his account of a new construction theory for such groups (5). We shall have frequent occasion to refer to these papers, and we begin with a brief account of their contents.

In this paper we consider the theory of point-curve correspondences on a single surface F, i.e. correspondences in which to each point of F corresponds an algebraic curve of F. The results previously obtained for induced and extended correspondences between two surfaces require some modification here, as we can consider the self-correspondences induced on a curve C of F, and the related theory of extended correspondences, which is now complicated by the existence of the identical correspondence on C. We also develop a theory of correspondences with (non-zero) valency, and show that for a surface whose Riemann matrix is pure and without complex multiplication (and hence for surfaces of ‘general moduli’), all correspondences are valency correspondences, this result being exactly analogous to the well-known theorem for curves. We also consider generalized valency correspondences which are an extension to surfaces of the concept of correspondences of multiple valency on a curve. The analogy between our theory and the known results for curves does break down in one important respect. It is not true that every surface possesses valency correspondences even of the generalized kind, the existence of such correspondences involving restrictions on the intersection group of the surface.

1. Let {μn} be a sequence of positive numbers increasing to infinity. If the series

converges for s > 0, and if f(s) → l as s → 0, then ∑an is said to be summable (A, μn) to l; this generalization of Abel summability, first introduced by Hardy, has long been familiar. Suppose that, for x ≥ μ0, ø(x)is a positive increasing function of x, which tends to infinity as x → ∞. We write throughout λn = ø(μn), and

if this exists.

This paper is the sequel to one entitled ‘An Inequality in the Theory of Arithmetic on Algebraic Varieties’ (1). For the definition of the complexity of an algebraic point P—here denoted by C[P]—we refer the reader to that paper, where he will also find a short account of as much of the theory of ‘distributions’ as will be used here. For full details of the latter, the reader should consult A. Weil's article (2). Both this paper and the preceding one are the result of an attempt to generalize and simplify a few of the many fruitful ideas which are embodied in Weil's thesis.

A function f(x1, x2) of two real variables x1, x2 which are restricted to rational integers will be called discrete harmonic (d.h.) if it satisfies the difference equation

This equation can be considered as the direct analogue either of the differential equation

or of the integral equation

in the notation normally employed to harmonic functions.

The determinantal quartic primal in [4], represented on [3] by quartic surfaces passing through a decimic curve of genus eleven, has already been the subject of a number of papers. The primal for which the base curve is a general curve C10 has twenty nodes, mapped by the twenty quadrisecant lines of the curve. If the C10 breaks up into a number of curves of lower order, the primal has, in addition, other nodes, mapped by the neighbourhoods of the intersections of two simple branches of the base curve. When the C10 consists of ten lines, having twenty mutual intersections to preserve the virtual genus eleven, the primal has forty nodes; the two primals of this type which contain no planes are the subject of a paper by Todd (3). Further specialization of the ten lines, giving more additional nodes, is possible; it has been shown in another paper (Todd (4)) that there is a quartic primal with forty-five nodes (the maximum number) which is determinantal. The figure in [3] formed by the base curve is described there; for a description of the configuration formed by the nodes in [4], and many other interesting properties of this primal, the reader is referred to two recent works (Baker (1) and Todd (5)). Further details about the general quartic primal, and references to a number of special cases, may be found in Room (2), chapters XV and XVI.

1. The quadrics of space are linearly dependent on ten among them; any ten linearly independent quadrics may be chosen to constitute the base, but it is customary in analytical work to select the four squares and the six products of pairs of four planes which are the faces of some tetrahedron of reference. This choice is adequate enough for many purposes, but it gives an unsymmetrical twist to the work; whereas four quadrics of the base are repeated planes the other six are plane pairs, and the curve common to two of the ten base quadrics can be a skew quadrilateral, a repeated line-pair, or a line counted four times. This radical defect can be mitigated by taking as base a certain set of ten non-singular quadrics, namely, the set of ten fundamental quadrics which is so prominent a feature of Klein's figure of six mutually apolar linear complexes. Every pair of such a set of ten quadrics has its two members related to one another in precisely the same way; their common curve is a skew quadrilateral and they are their own polar reciprocals with respect to each other.

The essential elements in any application of statistical theory are

(1) the set of hypothetical physical states θ which may give rise to the observed phenomena,

(2) the set of all possible observations or samples x,

(3) the set of actions α which may be taken when x is known.

The whole procedure in the common applications can be divided into two parts:

(A) the estimation of θ from the known observation x,

(B) action on the basis of this estimation.