Hostname: page-component-586b7cd67f-2brh9 Total loading time: 0 Render date: 2024-11-23T06:51:47.203Z Has data issue: false hasContentIssue false
  • English
  • Français

The cardinal series in Hilbert space

Published online by Cambridge University Press:  24 October 2008

J. D. Weston
J. D. Weston
Affiliation:
The UniversitySheffield
Get access Rights & Permissions [Opens in a new window]

Extract

The name ‘cardinal function’ was given to

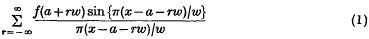
by E. T. Whittaker (1), who considered it as a ‘smooth’ approximation to a function f(x), having the same values as f(x) at the points a + rw (r = 0, ± 1, ± 2, …). It has since been extensively studied (2), mainly from the point of view of interpolation theory. Hardy (3), however, observed that the functions νr(t) defined by

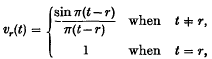
form a normal orthogonal set on the interval (−∞, ∞), for r = 0, ± 1, ± 2, …. This fact suggests a discussion of the cardinal series from the point of view of mean-square approximation.

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 45 , Issue 3 , July 1949 , pp. 335 - 341
Copyright
Copyright © Cambridge Philosophical Society 1949

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

(1)Whittaker, E. T.On the functions which are represented by the expansions of the interpolation theory. Proc. Roy. Soc. Edinburgh, 35 (1915), 181–94.Google Scholar
(2)Whittaker, J. M.Interpolatory Function Theory (Cambridge, 1935).Google Scholar
(3)Hardy, G. H.Notes on special systems of orthogonal functions. IV. Proc. Cambridge Phil. Soc. 37 (1941), 331–48.CrossRefGoogle Scholar
(4)Weston, J. D.A note on the theory of communication. Phil. Mag. (7) 40 (1949), 449–53.CrossRefGoogle Scholar
(5)Whittaker, J. M.On the cardinal function of interpolation theory. Proc. Edinburgh Math. Soc. (2), 1 (1929), 41–6.CrossRefGoogle Scholar
(6)Ferrar, W. L.On the cardinal function of interpolation theory. Proc. Roy. Soc. Edinburgh, 46 (1925), 323–33.Google Scholar
(7)Hardy, G. H.On an integral equation. Proc. London Math. Soc. 7 (1909), 445–72.CrossRefGoogle Scholar
(8)Copson, E. T.On Hardy's theory of m-functions. Proc. Edinburgh Math. Soc. (2), 1 (1929), 129–34.CrossRefGoogle Scholar