Research Article
Simultaneous Diophantine approximation in the real, complex and p–adic fields.
-
- Published online by Cambridge University Press:
- 10 May 2010, pp. 193-216
-
- Article
- Export citation
Bounds on fewnomial exponential sums over ℤp
-
- Published online by Cambridge University Press:
- 22 June 2010, pp. 217-227
-
- Article
- Export citation
Partial Castelnuovo–Mumford regularities of sums and intersections of powers of monomial ideals
-
- Published online by Cambridge University Press:
- 16 March 2010, pp. 229-246
-
- Article
- Export citation
The cl-core of an ideal
-
- Published online by Cambridge University Press:
- 03 June 2010, pp. 247-262
-
- Article
- Export citation
Invariants of 3-manifolds derived from covering presentations
-
- Published online by Cambridge University Press:
- 10 May 2010, pp. 263-295
-
- Article
- Export citation
The spiral index of knots
-
- Published online by Cambridge University Press:
- 04 June 2010, pp. 297-315
-
- Article
- Export citation
On the volume of caps and bounding the mean-width of an isotropic convex body
-
- Published online by Cambridge University Press:
- 10 May 2010, pp. 317-331
-
- Article
- Export citation
Aperiodicity and cofinality for finitely aligned higher-rank graphs†
-
- Published online by Cambridge University Press:
- 10 May 2010, pp. 333-350
-
- Article
- Export citation
Diamond aggregation
-
- Published online by Cambridge University Press:
- 10 May 2010, pp. 351-372
-
- Article
- Export citation
On the stability of the set of hyperbolic closed orbits of a Hamiltonian
-
- Published online by Cambridge University Press:
- 03 June 2010, pp. 373-383
-
- Article
- Export citation
Front Cover (OFC, IFC) and matter
PSP volume 149 issue 2 Cover and Front matter
-
- Published online by Cambridge University Press:
- 27 July 2010, pp. f1-f2
-
- Article
-
- You have access
- Export citation
Back Cover (IBC, OBC) and matter
PSP volume 149 issue 2 Cover and Back matter
-
- Published online by Cambridge University Press:
- 27 July 2010, pp. b1-b2
-
- Article
-
- You have access
- Export citation


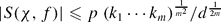 . If
. If 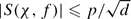 , and if
, and if 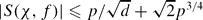 .
.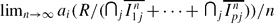 also exist.
also exist.