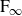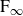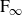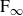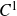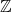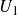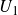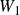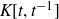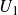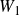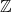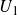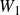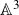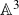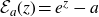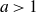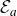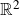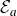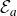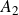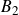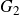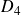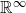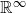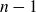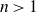Research Article
Dilogarithm identities after Bridgeman
- Part of:
-
- Published online by Cambridge University Press:
- 03 March 2022, pp. 1-23
-
- Article
- Export citation
The BNSR-invariants of the Lodha–Moore groups, and an exotic simple group of type
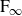 $\textrm{F}_\infty$
$\textrm{F}_\infty$
- Part of:
-
- Published online by Cambridge University Press:
- 04 April 2022, pp. 25-48
-
- Article
- Export citation
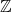 $\mathbb{Z}$
-graded identities of the Lie algebras
$\mathbb{Z}$
-graded identities of the Lie algebras
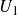 $U_1$
in characteristic 2
$U_1$
in characteristic 2
- Part of:
-
- Published online by Cambridge University Press:
- 08 March 2022, pp. 49-58
-
- Article
- Export citation
Asymptotic identities for additive convolutions of sums of divisors
-
- Published online by Cambridge University Press:
- 01 April 2022, pp. 59-78
-
- Article
- Export citation
Counting H-free orientations of graphs
- Part of:
-
- Published online by Cambridge University Press:
- 25 April 2022, pp. 79-95
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Higher rank motivic Donaldson–Thomas invariants of
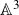 $\mathbb A^3$
via wall-crossing, and asymptotics
$\mathbb A^3$
via wall-crossing, and asymptotics
- Part of:
-
- Published online by Cambridge University Press:
- 05 May 2022, pp. 97-122
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Dynamics of generalised exponential maps
- Part of:
-
- Published online by Cambridge University Press:
- 21 April 2022, pp. 123-136
-
- Article
- Export citation
Groups generated by two twists along spherical sequences
- Part of:
-
- Published online by Cambridge University Press:
- 16 May 2022, pp. 137-161
-
- Article
- Export citation
Decoupling Decorations on Moduli Spaces of Manifolds
- Part of:
-
- Published online by Cambridge University Press:
- 10 May 2022, pp. 163-198
-
- Article
- Export citation
A table of n-component handlebody links of genus n+1 up to six crossings
- Part of:
-
- Published online by Cambridge University Press:
- 17 June 2022, pp. 199-223
-
- Article
- Export citation
Front Cover (OFC, IFC) and matter
PSP volume 174 issue 1 Cover and Front matter
-
- Published online by Cambridge University Press:
- 19 December 2022, pp. f1-f2
-
- Article
-
- You have access
- Export citation
Back Cover (OBC, IBC) and matter
PSP volume 174 issue 1 Cover and Back matter
-
- Published online by Cambridge University Press:
- 19 December 2022, pp. b1-b2
-
- Article
-
- You have access
- Export citation