Hostname: page-component-745bb68f8f-d8cs5 Total loading time: 0 Render date: 2025-02-10T23:24:29.001Z Has data issue: false hasContentIssue false
  • English
  • Français

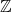$\mathbb{Z}$-graded identities of the Lie algebras 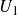$U_1$ in characteristic 2

Part of: Rings with polynomial identity Lie algebras and Lie superalgebras

Published online by Cambridge University Press:  08 March 2022

CLAUDEMIR FIDELIS  and
PLAMEN KOSHLUKOV
CLAUDEMIR FIDELIS
Affiliation:
Unidade Acadêmica de Matemática, Universidade Federal de Campina Grande, 785 Aprígio Veloso, Bodocongó, P.O.Box: 10044, Campina Grande, PB, 58429-970, Brazil Instituto de Matemática e Estatística, Universidade de São Paulo, São Paulo, SP, 05508-090, Brazil. e-mail: [email protected]
PLAMEN KOSHLUKOV
Affiliation:
Department of Mathematics, UNICAMP, 651 Sergio Buarque de Holanda, 13083-859 Campinas, SP, Brazil. e-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Let K be any field of characteristic two and let 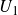$U_1$ and 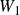$W_1$ be the Lie algebras of the derivations of the algebra of Laurent polynomials 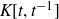$K[t,t^{-1}]$ and of the polynomial ring K[t], respectively. The algebras 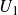$U_1$ and 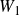$W_1$ are equipped with natural 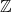$\mathbb{Z}$ -gradings. In this paper, we provide bases for the graded identities of 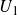$U_1$ and 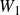$W_1$ , and we prove that they do not admit any finite basis.

MSC classification

Primary: 16R10: $T$-ideals, identities, varieties of rings and algebras
Secondary: 17B01: Identities, free Lie (super)algebras 17B65: Infinite-dimensional Lie (super)algebras 17B66: Lie algebras of vector fields and related (super) algebras 17B70: Graded Lie (super)algebras
Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 174 , Issue 1 , January 2023 , pp. 49 - 58
Copyright
© The Author(s), 2022. Published by Cambridge University Press on behalf of Cambridge Philosophical Society

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

†

Supported by FAPESP grant No. 2019/12498-0.

‡

Partially supported by FAPESP grant No. 2018/23690-6 and by CNPq grant No. 302238/2019-0.

References

AZEVEDO, S. S.. Graded identities for the matrix algebra of order n over an infinite field. Commun. Algebra (12) 30 (2002), 5849–5860.Google Scholar
AZEVEDO, S. S.. A basis for $\mathbb{Z}$ -graded identities of matrices over infinite fields. Serdica Math. J. 29 (2003), 149–158.Google Scholar
BAHTURIN, JU. A. and OL’SHANSKY., A. J. Identical relations in finite Lie rings. Math. USSR Sb. (4) 96 (138) (1975), 543–559. (Russian; English translation: Mathematics of the USSR-Sbornik, 25: 507-523.)CrossRefGoogle Scholar
BAHTURIN, Y., SEHGAL, S. and ZAICEV, M.. Group gradings on associative algebras. J. Algebra 241 (2001), 677–698.Google Scholar
BAHTURIN, Y. and ZAICEV, M.. Graded algebras and graded identities. Polynomial identities and combinatorial methods (Pantelleria, 2001). Lecture Notes in Pure and Appl. Math. vol. 235 (Dekker, New York, 2003), pp. 101–139.CrossRefGoogle Scholar
DE CONCINI, C. and PROCESI, C.. A characteristic free approach to invariant theory. Adv. Math. 21 (1976), 330–354.Google Scholar
DRENSKY, V.. Free algebras and PI algebras. Graduate course in Algebra (Springer-Verlag, Singapore 2000).Google Scholar
FIDELIS, C. and KOSHLUKOV, P.. $\mathbb{Z}$ -graded identities of the Lie algebras $U_1$ , submitted. arXiv preprint, arXiv:2107.10903v1 (2021).CrossRefGoogle Scholar
FREITAS, J. A., KOSHLUKOV, P. and KRASILNIKOV, A.. $\mathbb{Z}$ -graded identities of the Lie algebra $W_1$ . J. Algebra 427 (2015), 226–251.Google Scholar
GIAMBRUNO, A. and ZAICEV, M.. Polynomial identities and asymptotic methods. AMS Math. Surveys Monogr. vol. 122 (Providence, R.I., 2005).CrossRefGoogle Scholar
HUANG, Q. and ZHDANOV, R.. Realizations of the Witt and Virasoro algebras and integrable equations. J. Nonlinear Math. Phys. (1) 27 (2020), 36–56.Google Scholar
KAC, V.. Simple irreducible graded Lie algebras of finite growth. Izv. Akad. Nauk USSR, Ser. Mat. 32 (l968), 1923–1967. Transl. Math. USSR Izv. 2 (l968), 1271–1311.CrossRefGoogle Scholar
KAC, V.. Infinite-Dimensional Lie Algebras. 3rd ed. (Cambridge University Press, 1994).Google Scholar
KAPLANSKY, I.. The Virasoro algebra. Commun. Math. Phys. (1) 86 (1982), 49–54.CrossRefGoogle Scholar
KEMER, A. R.. Ideals of identities of associative algebras. Trans. Math. Monogr. vol. 87. (Amer. Math. Soc., Providence, RI, 1991).Google Scholar
KOSHLUKOV, P.. Basis of the identities of the matrix algebra of order two over a field of characteristic $p\ne 2$ . J. Algebra 241 (2001), 410–434.CrossRefGoogle Scholar
KOSHLUKOV, P. and AZEVEDO, S.. A basis for the graded identities of the matrix algebra of order two over a finite field of characteristic $p\neq 2$ . Finite Fields Appl. (4) 8 (2002), 597–609.Google Scholar
KOSHLUKOV, P. and YUKIHIDE, F.. Group gradings on the Lie algebra of upper triangular matrices. J. Algebra 477 (2017), 294–311.CrossRefGoogle Scholar
KOZYBAEV, D. and UMIRBAEV, U.. Identities of the left-symmetric Witt algebras. Internat. J. Algebra Comput. (2) 26 (2016), 435–450.Google Scholar
KRUSE, R. L.. Identities satisfied by a finite ring. J. Algebra 26 (1973), 298–318.CrossRefGoogle Scholar
KUKIN, G.P.. Bases of free Lie algebras. Mat. Zametki (3) 24 (1978), 375–382 (Russian). English translation: Math. Notes 24 (1979), 700–704.Google Scholar
LVOV, I. V.. Varieties of associative rings. Algebra i Logika (3) 12 (1973), 269–297 (Russian). English translation: Algebra Logic 12 (3) (1973), 150–167.Google Scholar
MATHIEU, O.. Classification of simple graded Lie algebras of finite growth. Invent. Math. (3) 108 (1992), 455–589.Google Scholar
OATES, S. and PPWELL, M. B.. Identical relations in finite groups. J. Algebra 1 (1964), 11–39.Google Scholar
POPOV, A.. Identities of the tensor square of a Grassmann algebra. Algebra i Logika (4) 21 (1982), 442–471 (Russian); English translation: Algebra and Logic 21 (1982), 296–316.Google Scholar
RAZMYSLOV, Yu.. Identities of algebras and their representations. Trans. Math. Monogr. vol. 138 (Amer. Math. Soc. Providence, RI, 1994).CrossRefGoogle Scholar
VASILOVSKY, S.. The basis of identities of a three-dimensional simple Lie algebra over an infinite field. Algebra i Logika (5) 28 (1989), 534–554 (Russian); English translation: Algebra Logic 28, No. 5 (1989), 355–368.Google Scholar
VASILOVSKY, S. Yu. $\mathbb{Z}$ -graded polynomial identities of the full matrix algebra. Commun. Algebra (2) 26 (1998), 601–612.Google Scholar
VASILOVSKY, S. Yu. $\mathbb{Z}_{n}$ -graded polynomial identities of the full matrix algebra of order n. Proc. Amer. Math. Soc. (12) 127 (1999), 3517–3524.Google Scholar