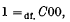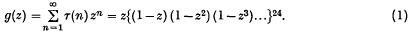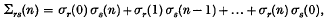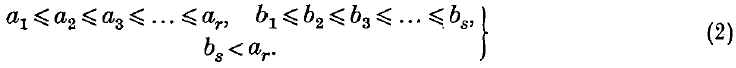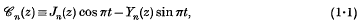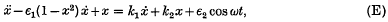Research Article
A formalization of the C-O propositional calculus
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 635-636
-
- Article
- Export citation
On multiplicative systems defined by generators and relations: I. Normal form theorems
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 637-649
-
- Article
- Export citation
Finite rotation groups and crystal classes in four dimensions
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 650-661
-
- Article
- Export citation
Some properties of analytically irreducible geometric quotient rings
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 662-667
-
- Article
- Export citation
On the order of magnitude of Ramanujan's arithmetical function τ(n)
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 668-678
-
- Article
- Export citation
On some new types of partitions associated with generalized ferrers graphs
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 679-686
-
- Article
- Export citation
Parametric surfaces: I. Area
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 687-698
-
- Article
- Export citation
A further method for the evaluation of zeros of Bessel functions and some new asymptotic expansions for zeros of functions of large order
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 699-712
-
- Article
- Export citation
Non-measurable interpolation sets: I. Integral functions
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 713-732
-
- Article
- Export citation
Non-measurable interpolation sets: II. functions regular in an angle
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 733-740
-
- Article
- Export citation
Periodic solutions of non-linear differential equations of the second order. IV
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 741-751
-
- Article
- Export citation
Periodic solutions of non-linear differential equations of the second order. V
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 752-755
-
- Article
- Export citation
Random motion on a finite Abelian group
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 756-762
-
- Article
- Export citation
Some geometrical properties of plane flows
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 763-776
-
- Article
- Export citation
The energy loss of free magnetic poles in passing through matter
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 777-789
-
- Article
- Export citation
On the statistical distribution of the widths and spacings of nuclear resonance levels
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 790-798
-
- Article
- Export citation
Statistics of the simple cubic lattice. II
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 799-810
-
- Article
- Export citation
Superconductivity of tin isotopes
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 811-819
-
- Article
- Export citation
Research Notes
A remark on the class number of quadratic forms of given determinant
-
- Published online by Cambridge University Press:
- 24 October 2008, p. 820
-
- Article
- Export citation
The dual recurrence relation for multiplicative processes
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 821-825
-
- Article
- Export citation