Research Article
The eighty-one types of isohedral tilings in the plane
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 177-196
-
- Article
- Export citation
A commutative Noetherian ring which possesses a dualizing complex is acceptable
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 197-213
-
- Article
- Export citation
A dual approach to Černikov modules
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 215-239
-
- Article
- Export citation
Primitive irreducible representations of nilpotent groups
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 241-247
-
- Article
- Export citation
Exact sequences of conjugacy classes and rationalization
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 249-253
-
- Article
- Export citation
The positive-definiteness of the complete symmetric functions of even order
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 255-258
-
- Article
- Export citation
Fully admissible binary relations in topology
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 259-264
-
- Article
- Export citation
The number of non-homogeneous lattice points in subsets of Rn
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 265-268
-
- Article
- Export citation
The eigenvalue problem for infinite systems of linear equations
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 269-273
-
- Article
- Export citation
The Riemann integrability of f′2 + g′2, f′, g′
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 275-276
-
- Article
- Export citation
Singular infinitely divisible distributions whose characteristic functions vanish at infinity
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 277-287
-
- Article
- Export citation
Some further results in infinite divisibility
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 289-295
-
- Article
- Export citation
On representation of Poisson mixtures as Poisson sums and a characterization of the gamma distribution
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 297-300
-
- Article
- Export citation
A counterexample to R. Davidson's conjecture on line processes
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 301-307
-
- Article
- Export citation
A new approach to subcritical instability and turbulent transitions in a simple dynamo
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 309-325
-
- Article
- Export citation
Scattering from infinite sheets
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 327-334
-
- Article
- Export citation
The static–geometric analogy in the equations of thin shell structures
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 335-351
-
- Article
- Export citation
Front matter
PSP volume 82 issue 2 Cover and Front matter
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. f1-f2
-
- Article
-
- You have access
- Export citation
Back matter
PSP volume 82 issue 2 Cover and Back matter
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. b1-b2
-
- Article
-
- You have access
- Export citation

 = {
= {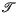 is called
is called 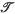 . Clearly every monohedral tiling is locally finite.
. Clearly every monohedral tiling is locally finite.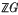 . Suppose that
. Suppose that 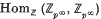 of a quasi-cyclic
of a quasi-cyclic 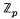 of
of 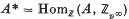 is a free
is a free 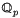 of
of 
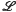 , other than the
, other than the 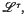 , and which is such that for any continuous mapping
, and which is such that for any continuous mapping 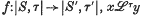 implies
implies 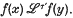 . With each such relation
. With each such relation 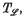 , as well as ‘
, as well as ‘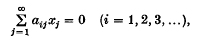
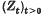 of symmetric random variables which satisfy
of symmetric random variables which satisfy 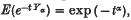 ,
, 
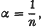 , where
, where 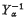 is distributed as the product of
is distributed as the product of