In earlier papers Kendall and Le[3,4] made a geometrical study of the structure and singularities of a convex-polygonally generated shape-density 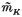 for any convex polygon K. The present work describes the singular tessellation T(K) in algebraic terms, and obtains explicit formulae for the ‘jump functions’ of m̃ across every edge of the tessellation. These results, combined with earlier work by Le[5] on the basic tile, make it possible to find m̃ explicitly in every tile by what we have called the ‘stepping-stone’ method. In a closing section the exact order of the differential singularity is found at the tile boundaries.
for any convex polygon K. The present work describes the singular tessellation T(K) in algebraic terms, and obtains explicit formulae for the ‘jump functions’ of m̃ across every edge of the tessellation. These results, combined with earlier work by Le[5] on the basic tile, make it possible to find m̃ explicitly in every tile by what we have called the ‘stepping-stone’ method. In a closing section the exact order of the differential singularity is found at the tile boundaries.

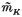 for any convex polygon
for any convex polygon