We prove Manin's conjecture for four singular quartic del Pezzo surfaces over imaginary quadratic number fields, using the universal torsor method.

We prove that the regular hendecagon (11-gon) is constructible by marked ruler and compass.

We give new Casson–Gordon style obstructions for a two–component link to be topologically concordant to the Hopf link.

Hua domains, generalized Hua domains and Hua constructions, named after the great Chinese mathematician Luogeng Hua (Loo-Keng Hua), are generalizations of Cartan–Hartogs domains introduced by Weiping Yin around the end of the 20th century. In this paper, we give a complete description of automorphism groups of generalized Hua domains. We also discuss the corresponding problem for Hua constructions.

For a closed, oriented, odd dimensional manifold X, we define the rho invariant ρ(X,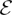${\cal E}$,H) for the twisted odd signature operator valued in a flat hermitian vector bundle 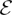${\cal E}$, where H = ∑ ij+1H2j+1 is an odd-degree closed differential form on X and H2j+1 is a real-valued differential form of degree 2j+1. We show that ρ(X,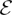${\cal E}$,H) is independent of the choice of metrics on X and 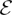${\cal E}$ and of the representative H in the cohomology class [H]. We establish some basic functorial properties of the twisted rho invariant. We express the twisted eta invariant in terms of spectral flow and the usual eta invariant. In particular, we get a simple expression for it on closed oriented 3-dimensional manifolds with a degree three flux form. A core technique used is our analogue of the Atiyah–Patodi–Singer theorem, which we establish for the twisted signature operator on a compact, oriented manifold with boundary. The homotopy invariance of the rho invariant ρ(X,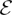${\cal E}$,H) is more delicate to establish, and is settled under further hypotheses on the fundamental group of X.

Necessary and sufficient conditions for the symbolic dynamics of a given Lorenz map to be fully embedded in the symbolic dynamics of a piecewise continuous interval map are given. As an application of this embedding result, we describe a new algorithm for calculating the topological entropy of a Lorenz map.

We introduce invariants of graphs embedded in S3 which are related to the Wu invariant and the Simon invariant. Then we use our invariants to prove that certain graphs are intrinsically chiral, and to obtain lower bounds for the minimal crossing number of particular embeddings of graphs in S3.

In this short paper, we use Robert Bruner's $\cal{A}$(1)-resolution of $P = {\mathbb{F}_2[t]$ to shed light on the Hit Problem. In particular, the reduced syzygies Pn of P occur as direct summands of $\widetilde{P}^{\otimes n}$, where $\widetilde{P}$ is the augmentation ideal of the map $P \to \mathbb{F}_2$. The complement of Pn in $\widetilde{P}^{\otimes n}$ is free, and the modules Pn exhibit a type of “Bott periodicity” of period 4: Pn+4 = Σ8Pn. These facts taken together allow one to analyse the module of indecomposables in $\widetilde{P}^{\otimes n}$, that is, to say something about the “$\cal{A}$(1)-hit Problem”. Our study is essentially in two parts: first, we expound on the approach to the Hit Problem begun by William Singer, in which we compare images of Steenrod squares to certain kernels of squares. Using this approach, the author discovered a nontrivial element in bidegree (5, 9) that is neither $\cal{A}$(1)-hit nor in kerSq1 + kerSq3. Such an element is extremely rare, but Bruner's result shows clearly why these elements exist and detects them in full generality; second, we describe the graded ${\mathbb{F}_2$-space of $\cal{A}$(1)-hit elements of $\widetilde{P}^{\otimes n}$ by determining its Hilbert series.

We give a lower bound on the Loewy length of a p-block of a finite group in terms of its defect. We then discuss blocks with small Loewy length. Since blocks with Loewy length at most 3 are known, we focus on blocks of Loewy length 4 and provide a relatively short list of possible defect groups. It turns out that p-solvable groups can only admit blocks of Loewy length 4 if p=2. However, we find (principal) blocks of simple groups with Loewy length 4 and defect 1 for all p ≡ 1 (mod 3). We also consider sporadic, symmetric and simple groups of Lie type in defining characteristic. Finally, we give stronger conditions on the Loewy length of a block with cyclic defect group in terms of its Brauer tree.