In this short paper, we use Robert Bruner's 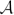$\cal{A}$(1)-resolution of $P = {\mathbb{F}_2[t]$ to shed light on the Hit Problem. In particular, the reduced syzygies Pn of P occur as direct summands of 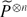$\widetilde{P}^{\otimes n}$, where 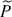$\widetilde{P}$ is the augmentation ideal of the map 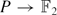$P \to \mathbb{F}_2$. The complement of Pn in 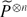$\widetilde{P}^{\otimes n}$ is free, and the modules Pn exhibit a type of “Bott periodicity” of period 4: Pn+4 = Σ8Pn. These facts taken together allow one to analyse the module of indecomposables in 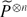$\widetilde{P}^{\otimes n}$, that is, to say something about the “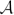$\cal{A}$(1)-hit Problem”. Our study is essentially in two parts: first, we expound on the approach to the Hit Problem begun by William Singer, in which we compare images of Steenrod squares to certain kernels of squares. Using this approach, the author discovered a nontrivial element in bidegree (5, 9) that is neither 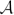$\cal{A}$(1)-hit nor in kerSq1 + kerSq3. Such an element is extremely rare, but Bruner's result shows clearly why these elements exist and detects them in full generality; second, we describe the graded 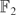${\mathbb{F}_2$-space of 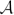$\cal{A}$(1)-hit elements of 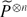$\widetilde{P}^{\otimes n}$ by determining its Hilbert series.