Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Prabhakar, Tilak Raj
1971.
Some Integral Equations with Rummer's Functions in the Kernels.
Canadian Mathematical Bulletin,
Vol. 14,
Issue. 3,
p.
391.
Buschman, R. G.
1972.
Decomposition of an Integral Operator by Use of Mikusiński Calculus.
SIAM Journal on Mathematical Analysis,
Vol. 3,
Issue. 1,
p.
83.
Prabhakar, Tilak Raj
1972.
Hypergeometric Integral Equations of a General Kind and Fractional Integration.
SIAM Journal on Mathematical Analysis,
Vol. 3,
Issue. 3,
p.
422.
Prabhakar, Tilak Raj
1972.
A Class of Integral Equations with Gauss Functions in the Kernels.
Mathematische Nachrichten,
Vol. 52,
Issue. 1-6,
p.
71.
Love, E. R.
Prabhakar, T. R.
and
Kashyap, N. K.
1982.
A confluent hypergeometric integral equation.
Glasgow Mathematical Journal,
Vol. 23,
Issue. 1,
p.
31.
Lamb, W.
1985.
A distributional theory of fractional calculus.
Proceedings of the Royal Society of Edinburgh: Section A Mathematics,
Vol. 99,
Issue. 3-4,
p.
347.
El-Sayed, Ahmed M A
1999.
On the generalized Laguerre polynomials of arbitrary (fractional) orders and quantum mechanics.
Journal of Physics A: Mathematical and General,
Vol. 32,
Issue. 49,
p.
8647.
Tarasov, Vasily E.
and
Tarasova, Svetlana S.
2020.
Fractional Derivatives and Integrals: What Are They Needed For?.
Mathematics,
Vol. 8,
Issue. 2,
p.
164.
Ghanim, F.
and
Al‐Janaby, Hiba F.
2021.
An analytical study on Mittag‐Leffler–confluent hypergeometric functions with fractional integral operator.
Mathematical Methods in the Applied Sciences,
Vol. 44,
Issue. 5,
p.
3605.
Ghanim, F.
Al-Janaby, Hiba F.
and
Bazighifan, Omar
2021.
Some New Extensions on Fractional Differential and Integral Properties for Mittag-Leffler Confluent Hypergeometric Function.
Fractal and Fractional,
Vol. 5,
Issue. 4,
p.
143.
Ghanim, Firas
Bendak, Salaheddine
and
Al Hawarneh, Alaa
2022.
Certain implementations in fractional calculus operators involving Mittag-Leffler-confluent hypergeometric functions.
Proceedings of the Royal Society A: Mathematical, Physical and Engineering Sciences,
Vol. 478,
Issue. 2258,
Tarasov, Vasily E.
2022.
Fractional Dynamics with Depreciation and Obsolescence: Equations with Prabhakar Fractional Derivatives.
Mathematics,
Vol. 10,
Issue. 9,
p.
1540.
Kukushkin, M. V.
2023.
Kipriyanov’s Fractional Calculus Prehistory and Legacy.
Lobachevskii Journal of Mathematics,
Vol. 44,
Issue. 8,
p.
3411.
Luchko, Yuri
2024.
On Symmetrical Sonin Kernels in Terms of Hypergeometric-Type Functions.
Mathematics,
Vol. 12,
Issue. 24,
p.
3943.
Ghanim, F.
Khan, Fareeha Sami
Al-Janaby, Hiba F.
and
Ali, Ali Hasan
2024.
A new hybrid special function class and numerical technique for multi-order fractional differential equations.
Alexandria Engineering Journal,
Vol. 104,
Issue. ,
p.
603.


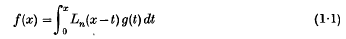
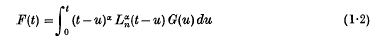
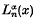 and Whittaker functions
and Whittaker functions 