Let N/K be a tame, abelian extension of number fields, whose Galois group is denoted by Γ. The basic object of study in this paper is the ring of integers of N, endowed with the trace form TN/K; the pair is then a Hermitian module (where we abbreviate ), and it restricts to a -Hermitian module (The reader is referred to Section 2 for the basics on Hermitian modules.) Ideally one would like to determine completely the class of this Hermitian module in K0H(ℤΓ), the Grothendieck group of ℤΓ-Hermitian modules modulo orthogonal sums; however, in general when Γ is even, one knows that even the ℚΓ-Hermitian module given by restricting (N, TN/K) is difficult to classify. (See for instance [S] and [F2].) To circumvent this difficulty we proceed in the following fashion, as suggested by the recent work of P. Lawrence (see [L]): let D = D(Γ) denote the anti-diagonal of Γ in Γ × Γ, that is to say

and let N(2) = (N⊗KN)D so that N(2) is a Galois algebra over K with Galois group Γ × Γ/D(Γ) ≅ Γ. Write for the trace form of N(2)/K, and define the -order it is then easy to see that is isomorphic as an -module to (see (3·1·6)). To be precise we ought really to write 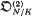etc.; however, the base field will always be clear from the context.