Let 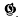be any transitive permutation group on the n symbols 1, …, n. Let 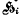be the subgroup of 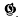whose elements leave i fixed. Let 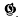′ be the normalizer of 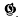, i.e., the subgroup of the symmetric group 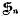on 1, …, n transforming 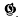into itself. Let G′, G′1, G′2, etc., denote elements of 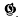′. Finally, let 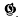″ be the centralizer of 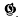, i.e., the subgroup in 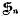transforming every element of 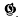into itself.