Hostname: page-component-586b7cd67f-2plfb Total loading time: 0 Render date: 2024-11-26T07:41:51.210Z Has data issue: false hasContentIssue false
  • English
  • Français

Symmetric amenability and the nonexistence of Lie and Jordan derivations

Published online by Cambridge University Press:  24 October 2008

B. E. Johnson
B. E. Johnson
Affiliation:
The University of Newcastle, Newcastle upon Tyne, NE1 7RU
Get access Rights & Permissions [Opens in a new window]

Extract

A. M. Sinclair has proved that if 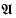is a semisimple Banach algebra then every continuous Jordan derivation from 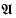into 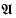is a derivation ([12, theorem 3·3]; ‘Jordan derivation’ is denned in Section 6 below). If 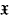is a Banach 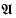-bimodule one can consider Jordan derivations from 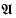into 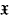and ask whether Sinclair's theorem is still true. More recent work in this area appears in [1]. Simple examples show that it cannot hold for all modules and all semisimple algebras. However, for more restricted classes of algebras, including C*-algebras one does get a positive result and we develop two approaches. The first depends on symmetric amenability, a development of the theory of amenable Banach algebras which we present here for the first time in Sections 2, 3 and 4. A Banach algebra is symmetrically amenable if it has an approximate diagonal consisting of symmetric tensors. Most, but not all, amenable Banach algebras are symmetrically amenable and one can prove results for symmetric amenability similar to those in [8] for amenability. However, unlike amenability, symmetric amenability does not seem to have a concise homological characterisation. One of our results [Theorem 6·2] is that if 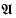is symmetrically amenable then every continuous Jordan derivation into an 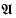-bimodule is a derivation. Special techniques enable this result to be extended to other algebras, for example all C*-algebras. This approach to Jordan derivations appears in Section 6.

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 120 , Issue 3 , October 1996 , pp. 455 - 473
Copyright
Copyright © Cambridge Philosophical Society 1996

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1]Bunce, L. J. and Wright, J. D. Maitland. Velocity maps in von Neumann algebras Pacific J. Math. 170 (1995), 421–427.Google Scholar
[2]Curtis, P. C. Jr, and Loy, R. J.. The structure of amenable Banach algebras. J. London Math. Soc. 2 (40) (1989), 89–104.CrossRefGoogle Scholar
[3]Dixmier, J.. Les C*-algebras et leurs représentations (Gauthier-Villars, 1964).Google Scholar
[4]Greenleaf, F. P.. Invariant means on topological groups and their applications (Van Nostrand Reinholt, 1969).Google Scholar
[5]Groenbaek, N.. A characterisation of weakly amenable Banach algebras. Studio, Mathematica 94 (1989), 149–162.Google Scholar
[6]Haagerup, U.. The Grothendiek inequality for bilinear forms on C*-algebras. Advances in Math. 56 (1985), 93–116.Google Scholar
[7]Helemskii, A. Ya.. Some remarks about ideas and results of topological homology. Proceedings of the conference on automatic continuity and Banach algebras, Canberra 1989, 203–238.Google Scholar
[8]Johnson, B. E.. Cohomology in Banach algebras. Mem. American Math. Soc. 127 (1972).Google Scholar
[9]Johnson, B. E.. Approximate diagonals and cohomology of certain annihilator Banach algebras. Amer. J. Math. 94 (1972), 685–698.CrossRefGoogle Scholar
[10]Kepert, A.. Amenability in group algebras and Banach algebras. Math. Scand. 74 (1994).CrossRefGoogle Scholar
[11]Selivanov, Yu. V.. Projectivity of certain Banach modules and the structure of Banach algebras. Soviet Math. (Iz VUZ) 22 (1978), 88–93.Google Scholar
[12]Sinclair, A. M.. Jordan homomorphisms and derivations on semisimple Banach algebras. Proc. American Math. Soc. 24 (1970), 209–214.Google Scholar