Hostname: page-component-586b7cd67f-r5fsc Total loading time: 0 Render date: 2024-11-29T19:37:06.724Z Has data issue: false hasContentIssue false
  • English
  • Français

The sums of powers as simultaneous canonical expressions

Published online by Cambridge University Press:  24 October 2008

J. Bronowski
J. Bronowski
Affiliation:
Jesus College
Get access Rights & Permissions [Opens in a new window]

Extract

1. In this paper I discuss the expression of m + 1 general forms F, F′, …, F(m), each of order n and homogeneous in r + 1 variables z0, z1, …, zl, …, zr, as the sums each of the nth powers of (the same) h + H linear forms in these variables. I take h > 0 of these linear forms to be undetermined, namely the forms

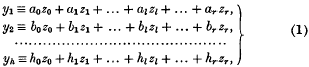
whose coefficients are undetermined; and I take the remaining H ≥ 0 linear forms to be assigned, namely the forms

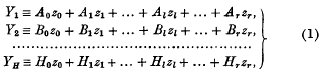
whose coefficients are assigned.

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 29 , Issue 2 , May 1933 , pp. 245 - 256
Copyright
Copyright © Cambridge Philosophical Society 1933

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

* This theorem is given by Terracini, A., Annali di Matematica (3), 24 (1915), 1CrossRefGoogle Scholar —a paper not known to me at the time the present paper was written. A. Terracini's paper also contains a proof of the well-known theorem of Em. Lasker and E. K. Wakeford, quoted by me in Proc. Camb. Phil. Soc. 29 (1933), 71Google Scholar; a reference to it should therefore be inserted in the footnote to that page.

† Richmond, H. W., Quart. J. of Math. 33 (1902), 331.Google Scholar

* See, for example, Salmon, G., Geometry of Three Dimensions, i, 5th edn. (1912), p. 242.Google Scholar

* For these and subsequent examples, see Severi, F., Rend. di Palermo, 15 (1901), 33.CrossRefGoogle Scholar

* Severi, F., Rend. di Palermo, 15 (1901), 33.CrossRefGoogle Scholar