Hostname: page-component-586b7cd67f-l7hp2 Total loading time: 0 Render date: 2024-11-26T13:44:15.799Z Has data issue: false hasContentIssue false
  • English
  • Français

Stability of a Column of Rotating Viscous Liquid

Published online by Cambridge University Press:  24 October 2008

J. Gillis
J. Gillis
Affiliation:
Weizmann Institute of ScienceRehovot, Israel
Get access Rights & Permissions [Opens in a new window]

Abstract

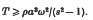A long column of viscous liquid of radius a and uniform density p is rotating about its axis with angular velocity ω. It is shown that this motion is stable to plane perturbations of wave number 8 provided that the surface tension T satisfies . This critical value is higher than that required for stability of the similar motion of a nonviscous liquid, but is otherwise independent of the coefficient of viscosity. The rate of development of instability when T is less than the critical value is also studied. Some numerical results are given.

The condition has recently been obtained by Hocking (2) for the special cases of very high and very low Reynolds numbers.

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 57 , Issue 1 , January 1961 , pp. 152 - 159
Copyright
Copyright © Cambridge Philosophical Society 1961

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

(1)Hocking, L. M., and Michael, D. H., Mathematika, 6 (1959), 25.CrossRefGoogle Scholar
(2)Hocking, L. M., Mathematika, 7 (1960), 1.CrossRefGoogle Scholar
(3)Watson, G. N., Theory of Bessel functions (Cambridge, 1952).Google Scholar