Hostname: page-component-cd9895bd7-lnqnp Total loading time: 0 Render date: 2024-12-30T21:47:33.096Z Has data issue: false hasContentIssue false
  • English
  • Français

Square-full numbers in short intervals

Published online by Cambridge University Press:  24 October 2008

D. R. Heath-Brown
D. R. Heath-Brown
Affiliation:
Magdalen College, Oxford
Get access Rights & Permissions [Opens in a new window]

Extract

A positive integer n is called square-full if p2|n for every prime factor p of n. Let Q(x) denote the number of square-full integers up to x. It was shown by Bateman and Grosswald [1] that

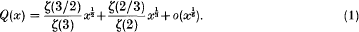
Bateman and Grosswald also remarked that any improvement in the exponent 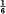would imply a ‘quasi-Riemann Hypothesis’ of the type 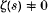for 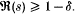. Thus (1) is essentially as sharp as one can hope for at present. From (1) it follows that, for the number of square-full integers in a short interval, we have

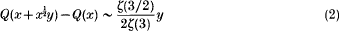
when 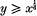and y = o (x½). (It seems more suggestive) to write the interval as (x, x + x½y]) than (x, x + y], since only intervals of length x½ or more can be of relevance here.)

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 110 , Issue 1 , July 1991 , pp. 1 - 3
Copyright
Copyright © Cambridge Philosophical Society 1991

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1]Bateman, P. T. and Grosswald, E.. On a theorem of Erdös and Szekeres. Illinois J. Math. 2 (1958), 88–98.CrossRefGoogle Scholar
[2]Jia, C-H.. The square-full integers in the short interval. Acta Math. Sinica 5 (1987), 614–621.Google Scholar
[3]Liu, H.. On square-full numbers in short intervals. Acta Math. Sinica 6 (1990), 148–164.Google Scholar
[4]Richert, H.-E.. Über die Anzahl Abelscher Gruppen gegebener Ordnung. I. Math. Z. 56 (1952), 21–32.CrossRefGoogle Scholar
[5]Shiu, P.. On square-full integers in a short interval. Glasgow Math. J. 25 (1984), 127–134.CrossRefGoogle Scholar