Published online by Cambridge University Press: 24 October 2008
Let {λn} be a sequence of non-negative numbers increasing to infinity. Let  be any series. Following the usual terminology, we say that the series is summable (R, λn, k) to s if
be any series. Following the usual terminology, we say that the series is summable (R, λn, k) to s if 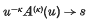 as u → ∞, where
as u → ∞, where  . If, further, u−kA(k)(u) is of bounded variation in (0, ∞), we say that the series is summable
. If, further, u−kA(k)(u) is of bounded variation in (0, ∞), we say that the series is summable 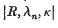 s. We say that the series is summable (A, λn) to s if
s. We say that the series is summable (A, λn) to s if  converges for all σ > 0, and tends to s as σ →0+. If A, B are two summability methods, we write A → B (‘A implies B’) if they have the property that any series summable A is necessarily summable B to the same sum.
converges for all σ > 0, and tends to s as σ →0+. If A, B are two summability methods, we write A → B (‘A implies B’) if they have the property that any series summable A is necessarily summable B to the same sum.
* Garabedian, H. L., Theorems associated with the Riesz and Dirichlet's series methods of summability, Bull. Amer. Math. Soc. 45 (1939), 891–5.CrossRefGoogle Scholar
† I am indebted to the referee for pointing this out.
‡ I use CM to denote Chandrasekharan, K. and Minakshisundaram, S., Typical means (Bombay, 1952).Google Scholar
* Widder, D. V., The Laplace transform (Princeton, 1941), 89 (Theorem 11·6b). In the theorem as stated by Widder, we put ![]() .Google Scholar
.Google Scholar
* To avoid repeated suffixes, we write λ(n) for λn whenever n is replaced by an expression which itself involves suffixes. We use a similar notation with other letters in place of λ.
† The notation given by (16) will be used throughout the paper.
* It is to ensure this that we have to take ![]() and not
and not ![]() .
.
† Here we appeal to Theorem 1·61 of CM rather than to the modification given by Lemma 2.
‡ Here and elsewhere a ‘turning point’ of a function is to be taken to mean a point at which its derivative vanishes.
* These equations determine uniquely the ratio of the b's.
* This is possible since (except in the trivial case in which all the relevant a's vanish) ![]() is not identically zero for
is not identically zero for ![]() . For if it were, we would have
. For if it were, we would have ![]() and any one of equations (49) shows that we would then also have
and any one of equations (49) shows that we would then also have ![]() .
.
† In the case m = 0, (48) is to be replaced by (47), and (52) omitted.