Hostname: page-component-cd9895bd7-jkksz Total loading time: 0 Render date: 2024-12-30T21:22:26.517Z Has data issue: false hasContentIssue false
  • English
  • Français

Some self-dual local rings of integers not free over their associated orders

Published online by Cambridge University Press:  24 October 2008

N. P. Byott
N. P. Byott
Affiliation:
New College, Oxford
Get access Rights & Permissions [Opens in a new window]

Extract

Let p be a prime number, and let K be a finite extension of the rational p-adic field ℚp. Let L/K be a finite abelian extension with Galois group G, and let 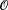L, 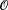K denote the valuation rings of L, K respectively. Then L is a free module of rank 1 over the group algebra KG. Defining the associated order 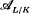of the extension L/K by

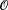L can be viewed as a module over the ring 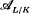, and a fortiori over the group ring 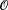KG.

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 110 , Issue 1 , July 1991 , pp. 5 - 10
Copyright
Copyright © Cambridge Philosophical Society 1991

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1]Bergé, A-M.. Arithmétique d'une extension galoisienne à groupe d'inertie cyclique. Ann. Inst. Fourier (Grenoble) 28 (1978), 17–44.CrossRefGoogle Scholar
[2]Burns, D.. Private communication with the author (1990).Google Scholar
[3]Cassou-Noguès, Ph. and Taylor, M. J.. Elliptic Functions and Rings of Integers. Progress in Mathematics vol. 66 (Birkhauser, 1987).Google Scholar
[4]Ferton, M. J.. Sur les idéaux d'une extension cyclique de degré premier d'un corps local. C. R. Acad. Sci. Paris 276 (1973), A1483–A1486.Google Scholar
[5]Martel, B.. Sur l'anneau des entiers d'une extension biquadratique d'un corps 2-adique. C. R. Acad. Sci. Paris 278 (1974), A117–A120.Google Scholar
[6]Serre, J-P.. Local Fields. Graduate Texts in Mathematics no. 67 (Springer-Verlag, 1979).CrossRefGoogle Scholar
[7]Washington, L. C.. Introduction to Cyclotomic Fields. Graduate Texts in Mathematics no. 83 (Springer-Verlag, 1982).CrossRefGoogle Scholar