Hostname: page-component-cd9895bd7-dzt6s Total loading time: 0 Render date: 2024-12-28T14:34:58.765Z Has data issue: false hasContentIssue false
  • English
  • Français

Some physical interpretations of potentials representing supersonic motion of compressible fluids

Published online by Cambridge University Press:  24 October 2008

R. K. Tempest
R. K. Tempest
Affiliation:
Department of Applied MathematicsThe UniversityLiverpool
Get access Rights & Permissions [Opens in a new window]

Extract

1. Compressible and incompressible flow. Small perturbations in an otherwise uniform stream of compressible fluid moving at supersonic speed are described by the approximate linearized equation for the velocity potential. When the stream flows in the z-direction, the equation assumes the form

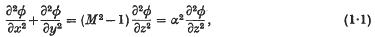
where M is the Mach number of the flow and α2 is positive. In cylindrical polar coordinates (r, z), the equation may be written as

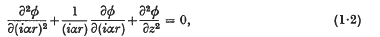
which is Laplace's equation in coordinates (iαr, z). We may therefore relate potentials of incompressible flow which are solutions of (1·2) to potentials of compressible flow which are solutions of (1·1).

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 45 , Issue 2 , April 1949 , pp. 246 - 250
Copyright
Copyright © Cambridge Philosophical Society 1949

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

(1)von Kármán, T. and Moore, N. B.Trans. American Soc. Mech. Engrs, 54 (1932), 303–10.Google Scholar
(2)Prandtl, L.Luftfahrtforschung, Vol. 13, no. 10 (1936), 313–19.Google Scholar
(3)Tsien, H. S.J. Aero. Sci. 5, no. 2 (1936), 480–3.Google Scholar
(4)Lighthill, M. J.Rep. Memor. Aero. Res. Comm., Lond., no. 2001 (1944).Google Scholar