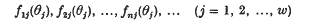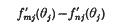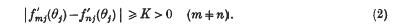Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Cassels, J. W. S.
1951.
An extension of the law of the iterated logarithm.
Mathematical Proceedings of the Cambridge Philosophical Society,
Vol. 47,
Issue. 1,
p.
55.
Schmidt, Wolfgang M.
1960.
A metrical theorem in geometry of numbers.
Transactions of the American Mathematical Society,
Vol. 95,
Issue. 3,
p.
516.
Schmidt, Wolfgang
1960.
A Metrical Theorem in Diophantine Approximation.
Canadian Journal of Mathematics,
Vol. 12,
Issue. ,
p.
619.
Schmidt, Wolfgang M.
1964.
Metrical theorems on fractional parts of sequences.
Transactions of the American Mathematical Society,
Vol. 110,
Issue. 3,
p.
493.
Baker, R. C.
1974.
Khinchin's conjecture and Marstrand's theorem.
Mathematika,
Vol. 21,
Issue. 2,
p.
248.
Baker, R. C.
1976.
Dyadic methods in the measure theory of numbers.
Transactions of the American Mathematical Society,
Vol. 221,
Issue. 2,
p.
419.
Nair, R.
1989.
On Leveque’s theorem about the uniform distribution (MOD 1) of (a j cosa jx) j =1/∞.
Israel Journal of Mathematics,
Vol. 65,
Issue. 1,
p.
96.
Dehling, Herold
and
Philipp, Walter
2002.
Empirical Process Techniques for Dependent Data.
p.
3.
Berkes, István
Philipp, Walter
and
Tichy, Robert F.
2007.
Pseudorandom numbers and entropy conditions.
Journal of Complexity,
Vol. 23,
Issue. 4-6,
p.
516.
Berkes, István
Philipp, Walter
and
Tichy, Robert F.
2008.
Diophantine Approximation.
Vol. 16,
Issue. ,
p.
95.
Aistleitner, Christoph
and
Berkes, Istvan
2009.
On the law of the iterated logarithm for the discrepancy of 〈n k x〉.
Monatshefte für Mathematik,
Vol. 156,
Issue. 2,
p.
103.
AISTLEITNER, CHRISTOPH
and
BERKES, ISTVÁN
2011.
PROBABILITY AND METRIC DISCREPANCY THEORY.
Stochastics and Dynamics,
Vol. 11,
Issue. 01,
p.
183.
Kleinbock, Dmitry
Shi, Ronggang
and
Weiss, Barak
2017.
Pointwise equidistribution with an error rate and with respect to unbounded functions.
Mathematische Annalen,
Vol. 367,
Issue. 1-2,
p.
857.
Lewko, Mark
and
Radziwiłł, Maksym
2017.
Refinements of Gál's theorem and applications.
Advances in Mathematics,
Vol. 305,
Issue. ,
p.
280.
Dietmann, Rainer
Fisher, Tom
Smyth, Chris
and
Velani, Sanju
2023.
John William Scott (‘Ian’) Cassels. 11 July 1922—27 July 2015.
Biographical Memoirs of Fellows of the Royal Society,
Vol. 74,
Issue. ,
p.
87.