A separable quasidiagonal C*-algebra with a non-quasidiagonal quotient by the compact operators
Published online by Cambridge University Press: 24 October 2008
Extract
A C*-algebra A of operators on a separable Hilbert space H is said to be quasidiagonal if there is an increasing sequence E1, E2, … of finite-rank projections on H tending strongly to the identity and such that
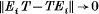
as i → ∞ for T∈A. More generally a C*-algebra is quasidiagonal if there is a faithful *-representation π of A on a separable Hilbert space H such that π(A) is a quasidiagonal algebra of operators. When this is the case, there is a decomposition H = H1 ⊕ H2 ⊕ … where dim Hi < ∞ (i = 1, 2,…) such that each T∈π(A) can be written T = D + K where D= D1 ⊕ D2 ⊕ …, with Di∈L(Hi) (i = 1, 2,…), and K is a compact linear operator on H. As is well known (and readily seen), this is an alternative characterization of quasidiagonality.
- Type
- Research Article
- Information
- Mathematical Proceedings of the Cambridge Philosophical Society , Volume 110 , Issue 1 , July 1991 , pp. 143 - 145
- Copyright
- Copyright © Cambridge Philosophical Society 1991
References
REFERENCES
- 2
- Cited by


