Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Isbell, John R.
1970.
Two examples in varieties of monoids.
Mathematical Proceedings of the Cambridge Philosophical Society,
Vol. 68,
Issue. 2,
p.
265.
Plotkin, B. I.
1973.
General theory of groups.
Journal of Soviet Mathematics,
Vol. 1,
Issue. 5,
p.
527.
Bergman, George M.
1981.
Hyperidentities of groups and semigroups.
Aequationes Mathematicae,
Vol. 23,
Issue. 1,
p.
50.
Baumslag, G.
and
Roitberg, Y.
1982.
Groups with free 2-generator subsemigroups.
Semigroup Forum,
Vol. 25,
Issue. 1,
p.
135.
Serajuddin, A. M.
1984.
The Chakma tribe of the Chittagong Hill Tracts in the 18th Century.
Journal of the Royal Asiatic Society of Great Britain & Ireland,
Vol. 116,
Issue. 1,
p.
90.
Gon�alves, J. Z.
and
Mandel, A.
1991.
Semigroup identities on units of group algebras.
Archiv der Mathematik,
Vol. 57,
Issue. 6,
p.
539.
Endimioni, G.
1995.
On a combinatorial problem in varieties of groups.
Communications in Algebra,
Vol. 23,
Issue. 14,
p.
5297.
Ol'shanskii, A. Yu.
and
Storozhev, A.
1996.
A group variety defined by a semigroup law.
Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics,
Vol. 60,
Issue. 2,
p.
255.
Burns, Robert G.
Macedońska, Olga
and
Medvedev, Yuri
1997.
Groups Satisfying Semigroup Laws, and Nilpotent-by-Burnside Varieties.
Journal of Algebra,
Vol. 195,
Issue. 2,
p.
510.
Longobardi, Patrizia
and
Maj, Mercede
1998.
On some classes of orderable groups.
Rendiconti del Seminario Matematico e Fisico di Milano,
Vol. 68,
Issue. 1,
p.
203.
Traustason, G.
1999.
Semigroup identities in 4-Engel groups.
Journal of Group Theory,
Vol. 2,
Issue. 1,
Macedońska, Olga
2000.
Collapsing groups and positive laws.
Communications in Algebra,
Vol. 28,
Issue. 8,
p.
3661.
Riley, David M.
2001.
Positively n-Engel groups.
Journal of Group Theory,
Vol. 4,
Issue. 4,
Kozhevnikov, P.
and
Macedońska, O.
2002.
ON VARIETIES OF GROUPS WITHOUT POSITIVE LAWS.
Communications in Algebra,
Vol. 30,
Issue. 9,
p.
4331.
Macedońska, O.
2002.
Two questions on semigroup laws.
Bulletin of the Australian Mathematical Society,
Vol. 65,
Issue. 3,
p.
431.
Endimioni, G.
2002.
Bounds for nilpotent-by-finite groups in certain varieties.
Journal of the Australian Mathematical Society,
Vol. 73,
Issue. 3,
p.
393.
Cain, Alan J
Robertson, Edmund F
and
Ruškuc, Nik
2006.
Subsemigroups of groups: presentations, Malcev presentations, and automatic structures.
jgth,
Vol. 9,
Issue. 3,
p.
397.
Macedońska, O.
2007.
On difficult problems and locally graded groups.
Journal of Mathematical Sciences,
Vol. 142,
Issue. 2,
p.
1949.
Macedońska, O.
and
Tomaszewski, W.
2011.
Groups St Andrews 2009 in Bath.
p.
461.
Słanina, Piotr
and
Zarzycki, Roland
2019.
Laws with constants in Thompson's group 𝐹.
Journal of Group Theory,
Vol. 22,
Issue. 5,
p.
783.


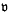 be a variety of groups. We say that the variety
be a variety of groups. We say that the variety 