Hostname: page-component-586b7cd67f-g8jcs Total loading time: 0 Render date: 2024-11-26T07:40:59.585Z Has data issue: false hasContentIssue false
  • English
  • Français

Schauder decompositions in locally convex spaces

Published online by Cambridge University Press:  24 October 2008

N. J. Kalton
N. J. Kalton
Affiliation:
University of Warwick
Get access Rights & Permissions [Opens in a new window]

Extract

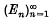A decomposition of a topological vector space E is a sequence of non-trivial subspaces of E such that each x in E can be expressed uniquely in the form 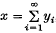, where yi∈Ei for each i. It follows at once that a basis 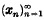of E corresponds to the decomposition consisting of the one-dimensional subspaces En = lin{xn}; the theory of bases can therefore be regarded as a special case of the general theory of decompositions, and every property of a decomposition may be naturally denned for a basis.

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 68 , Issue 2 , September 1970 , pp. 377 - 392
Copyright
Copyright © Cambridge Philosophical Society 1970

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

(1)Arsove, M. and Edwards, R.Generalised bases in topological linear spaces. Stud. Math. 19 (1958), 95–113.CrossRefGoogle Scholar
(2)Bennett, G. and Cooper, J. B.Weak bases in (F) and (LF)-spaces. J. Lond. Math. Soc. 175 (1969), 505–508.CrossRefGoogle Scholar
(3)Cook, T. A.Schauder decompositions and semi-reflexive spaces. Math. Ann. 182 (1969), 232–235.CrossRefGoogle Scholar
(4)Dubinsky, E. and Retherford, J. B.Schauder bases and Köthe sequence spaces. Trans. Amer. Math. Soc. 130 (1968), 265–280.Google Scholar
(5)Garling, D. J. H.The β- and γ-duality of sequence spaces. Proc. Cambridge Philos. Soc. 63 (1967), 963–981.CrossRefGoogle Scholar
(6)Garling, D. J. H.On topological sequence spaces. Proc. Cambridge Philos. Soc. 63 (1967), 997–1019.CrossRefGoogle Scholar
(7)James, R. C.Bases and reflexivity of Banach spaces. Ann. Math. 52 (1950), 518–527.CrossRefGoogle Scholar
(8)Kalton, N. J.Schauder decompositions and completeness. Bull. London Math. Soc. (in the Press).Google Scholar
(9)McArthur, C. W. and Retherford, J. R.Uniform and equicontinuous Schauder bases of subspaces. Can. J. Math. 17 (1965), 207–212.CrossRefGoogle Scholar
(10)Ruckle, W.The infinite sum of closed subspaces of an F-space. Duke Math. J. 31 (1964), 543–554.CrossRefGoogle Scholar
(11)Singer, I.Basic sequences and reflexivity of Banach spaces. Stud. Math. 21 (1962), 351–369.CrossRefGoogle Scholar